对实数a和b,定义运算“⊗”:a⊗b= ,设函数f(x)=(x2-2)⊗(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
,设函数f(x)=(x2-2)⊗(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A.(-∞,-2]∪ |
B.(-∞,-2]∪ |
C. ∪ ∪ |
D. ∪ ∪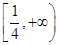 |
数据x1,x2,…,xn平均数为6,标准差为2,则数据2x1-6,2x2-6,…,2xn-6的平均数与方差分别为().
| A.6,16 | B.12,8 | C.6,8 | D.12,16 |
在△ABC中,AC=1,A=2B,则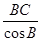 的值等于().
的值等于().
| A.3 | B.2 | C.1 | D.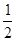 |
已知数列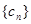 的通项是
的通项是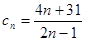 ,则数列
,则数列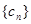 中的正整数项有()项.
中的正整数项有()项.
| A.1 | B.2 | C.3 | D.4 |
为了解儿子身高与父亲身高的关系,随机抽取了5对父子身高数据如下:
| 父亲身高x(cm) |
174 |
176 |
176 |
176 |
178 |
| 儿子身高y(cm) |
175 |
175 |
176 |
177 |
177 |
y对x的线性回归方程为().
A.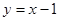 B.
B.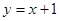 C.
C. D.
D.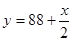
有下列调查方式:①学校为了解高一学生的数学学习情况,从每班抽2人进行座谈;②一次数学竞赛中,某班有15人在100分以上,35人在90~100分,10人低于90分。现在从中抽取12人座谈了解情况;③运动会中工作人员为参加400m比赛的6名同学公平安排跑道。就这三个调查方式,最合适的抽样方法依次为().
| A.分层抽样,系统抽样,简单随机抽样 |
| B.系统抽样,系统抽样,简单随机抽样 |
| C.分层抽样,简单随机抽样,简单随机抽样 |
| D.系统抽样,分层抽样,简单随机抽样 |