如图所示,一质量为M=1.2kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m。一质量为m=20g的子弹以水平速度v0=100m/s射入物块,在很短的时间内以水平速度穿出。已知物块落地点离桌面边缘的水平距离x为0.9m,取重力加速度g=10m/s2,求子弹穿出物块时速度v的大小。
如图是利用传送带装运煤块的示意图.其中,传送带足够长,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮轴顶端与运煤车底板间的竖直高度H=1.8m,与运煤车车箱中心的水平距离x=1.2m.现在传送带底端由静止释放一些煤块(可视为质点),煤块在传送带的作用下先做匀加速直线运动,后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.使煤块在轮的最高点恰好水平抛出并落在车箱中心,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
(1)传送带匀速运动的速度v
(2)主动轮和从动轮的半径R;
(3)煤块在传送带上由静止开始加速至与传送带速度相同所经过的时间t.
长L=0.5 m、质量可忽略的杆,其一端固定于O点,另一端连有质量m=2 kg的小球,它绕O点在竖直平面内做圆周运动.当通过最高点时,如图所示,求下列情况下,杆受到的力(计算出大小,并说明是拉力还是压力,g取10 m/s2):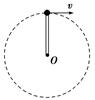
(1)当v=1 m/s时,杆受到的力多大,是什么力?
(2)当v=4 m/s时,杆受到的力多大,是什么力?
在双人花样滑冰比赛中,有时会看到被男运动员拉着的女运动员离开地面在空中做圆锥摆运动的精彩场面,质量为m的女运动员做圆锥摆运动时和水平冰面的夹角为θ,转动过程中女运动员的重心做匀速圆周运动的半径为r,重力加速度为g,求:
(1)该女运动员受到拉力的大小.
(2)该女运动员做圆锥摆运动的周期.
一架军用直升机悬停在距离地面64m的高处,将一箱军用物资由静止开始投下,如果不打开物资上的自动减速伞,物资经4s落地。为了防止物资与地面的剧烈撞击,须在物资距离地面一定高度时将物资上携带的自动减速伞打开。已知物资接触地面的安全限速为2m/s,减速伞打开后物资所受空气阻力是打
开前的18倍。忽略减速伞打开的时间,减速伞打开前后物资保持各自所受空气阻力不变,取g="10" m/s2。求
(1)减速伞打开前物资受到的空气阻力为自身重力的多少倍?
(2)减速伞打开时物资离地面的高度至少为多少?
如图所示,在倾角为37°的固定斜面上静置一个质量为5 kg的物体,物体与斜面间的动摩擦因数为0.8.求: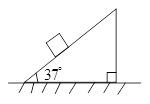
(1)物体所受的摩擦力;sin 37°=0.6,cos 37°=0.8
(2)若用原长为10 cm,劲度系数为3.1×103 N/m的弹簧沿斜面向上拉物体,使之向上匀速运动,则弹簧的最终长度是多少?取g=10 m/s2