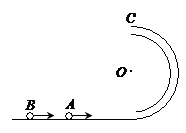
如图所示，传送带以一定速度沿水平方向匀速运动，将质量m＝1.0kg的小物块轻轻放在传送带上的P点，物块运动到A点后被水平抛出，小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑．B、C为圆弧的两端点，其连线水平，轨道最低点为O，已知圆弧对应圆心角θ＝106°，圆弧半径R＝1.0m，A点距水平面的高度h＝0.8m，小物块离开C点后恰好能无碰撞地沿固定斜面向上滑动，经过 0.8s小物块经过D点，已知小物块与斜面间的动摩擦因数μ＝.(取sin53°＝0.8，g＝10m/s2)求：
(1)小物块离开A点时的水平速度大小；
(2)小物块经过O点时，轨道对它的支持力大小；
(3)斜面上C、D间的距离．
一重力为mg的小球，用长为L的轻绳挂于O点，小球在水平拉力作用下，从平衡位置P点极其缓慢地移动到Q点，此时轻绳与竖直方位的夹角为600，。试求：
（1）小球从P点缓慢移到Q点的过程中，拉力所做的功；
（2）在Q点撤除外力，小球将会绕p点来回左右摆动，最终停止在P点，设在整个摆动的过程中空气阻力的平均大小为f，那么从撤去外力开始到最终停在P点的整个过程中，小球路程是多少？
以V0=12m∕s的初速度竖直向上抛出一质量为0.5kg的物体，g取10m/s2。。求:
（1）不考虑空气阻力，小球上升的最大高度和回到抛出点的时间；
（2）如果空气阻力f大小恒为1.0N，求小球回到抛出点时速度大小。
某一同学斜拉一质量为25kg的旅行箱，匀速地在机场的候车大厅内直线走了50m，如果拉力与水平面的夹角为370，旅行箱与地面的动摩擦因数为0.3，试计算(g取9.8m/s2,sin370=0.6,cos370=0.8)
(1) 拉力的大小和拉力做的功
(2) 摩擦力做的功
为了迎接太空时代的到来，美国国会通过了一项计划：在2050年前建造成太空升降机，就是把长绳的一端搁置在地球的卫星上，另一端系住升降机，放开绳，升降机能到达地球上，人坐在升降机里，在卫星上通过电动机把升降机拉到卫星上。已知地球表面的重力加速度g=10m/s2，地球半径R=6400km.当在地球表面时某人用弹簧测力计称得某物体重32N，站在升降机中，当升降机以加速度a=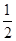
g（g为地球表面的重力加速度）竖直上升时，此人再一次用同一弹簧测力计称得同一物体重为18N，忽略地球公转的影响，求升降机此时距地面的高度。
如图所示，半径为R，内径很小的光滑半圆细管竖直放置，两个质量均为m的小球A、B，以不同的速率进入管内，若A球通过圆周最高点C，对管壁上部的压力为3mg，B球通过最高C时，对管壁内侧下部的压力为0.75mg，求A、B球落地点间的距离。