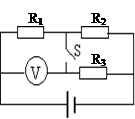
如图所示，一直立的汽缸用一质量为m的活塞封闭一定质量的理想气体，活塞横截面积为S，气体最初的体积为V0，气体最初的压强为p0/2，汽缸内壁光滑且缸壁是导热的。开始活塞被固定，打开固定螺栓K，活塞下落，经过足够长时间后，活塞停在B点，设周围环境温度保持不变，已知大气压强为p0，重力加速度为g。若一定质量理想气体的内能仅由温度决定，求：
①活塞停在B点时缸内封闭气体的体积V；
②整个过程中通过缸壁传递的热量Q。
汽车刹车进站，刹车前的速度为5m/s，刹车过程获得的加速度大小为0.4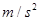
.求：
(1)汽车刹车开始后20秒内滑行的距离
；
(2)汽车停止运动前2s内滑行的距离
.
某同学为了测定气垫导轨上滑块的加速度，他在滑块上安装了宽度d=2cm的遮光板．然后他利用气垫导轨和数字毫秒计记录了遮光板通过第一个光电门所用的时间为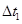
=0.1s，通过第二个光电门的时间
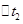=0.05s，遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为t=2.00s，请你根据上面他通过实验得到的数据，为他计算出滑块的加速度．
如图所示，两平行金属板相距为d，加上如图所示（b）所示的方波形电压，电压的最大值为U0，周期为T.现有重力可忽略的一束离子，每个离子的质量为m，电量为q，从与两板等距处的O点，沿着与板平行的方向连续地射入两板中。已知每个离子通过平行板所需的时间恰为T（电压变化周期）且所有离子都能通过两板间的空间，打在两金属板右端的荧光屏上，试求：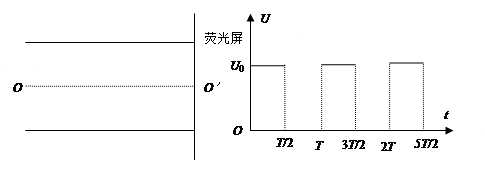
（1）离子打在荧光屏上的位置与O′点的最小距离
（2）离子打在荧光屏上的位置与O′点的最大距离。
一束电子流在经U＝2500 V的加速电压加速后，在距两极板等距处垂直进入平行板间的匀强电场，如图所示，若两板间距d="1.0" cm，板长l="5.0" cm，那么，要使二价负离子能从平行板间飞出，两个极板上最多能加多大电压?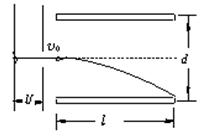
如图所示的电路中，
=3.5Ω,
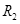=6Ω,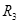
=3Ω，电压表为理想电表，当开关S断开时，电压表示数为5.7V；当开关S闭合时，电压表示数为3.5V，求电源的电动势和内电阻．