如图所示,杆OA长为R,可绕过O点的水平轴在竖直平面内转动,其端点A系 着一跨过定滑轮B、C的不可伸长的轻绳,绳的另一端系一物块M,滑轮的半径可忽略,B在O的正上方,OB之间的距离为H。某一时刻,当绳的BA段与OB之间的夹角为α=30°时,杆的角速度为ω,求此时物块M的速率 vM。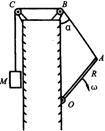
氢原子第n能级的能量为 ,其中E1是基态能量。而n=1,2,…。若一氢原子发射能量为
,其中E1是基态能量。而n=1,2,…。若一氢原子发射能量为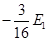 的光子后处于比基态能量高出
的光子后处于比基态能量高出 的激发态,则氢原子发射光子前后分别处于第几能级?
的激发态,则氢原子发射光子前后分别处于第几能级?
如图,置于空气中的一不透明容器内盛满某种透明液体。容器底部靠近器壁处有一竖直放置的6.0 cm长的线光源。靠近线光源一侧的液面上盖有一遮光板,另一侧有一水平放置的与液面等高的望远镜,用来观察线光源。开始时通过望远镜不能看到线光源的任何一部分。将线光源沿容器底向望远镜一侧平移至某处时,通过望远镜刚好可以看到线光源底端,再将线光源沿同一方向移动8.0 cm,刚好可以看到其顶端。求此液体的折射率n。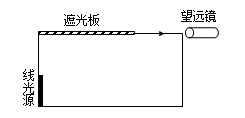
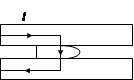
如图,在大气中有一水平放置的固定圆筒,它由a、b和c三个粗细不同的部分连接而成,各部分的横截面积分别为2S、 S和S。已知大气压强为p0,温度为T0.两活塞A和B用一根长为4l的不可伸长的轻线相连,把温度为T0的空气密封在两活塞之间,此时两活塞的位置如图所示。现对被密封的气体加热,使其温度缓慢上升到T。若活塞与圆筒壁之间的摩擦可忽略,此时两活塞之间气体的压强可能为多少?
S和S。已知大气压强为p0,温度为T0.两活塞A和B用一根长为4l的不可伸长的轻线相连,把温度为T0的空气密封在两活塞之间,此时两活塞的位置如图所示。现对被密封的气体加热,使其温度缓慢上升到T。若活塞与圆筒壁之间的摩擦可忽略,此时两活塞之间气体的压强可能为多少?
如图所示,一辆汽车A拉着装有集装箱的拖车B,以速度v1=30 m/s进入向下倾斜的直车道。车道每100 m下降2 m。为了使汽车速度在s=200 m的距离内减到v2=10 m/s,驾驶员必须刹车。假定刹车时地面的摩擦阻力是恒力,且该力的70%作用于拖车B,30%作用于汽车A。已知A的质量m1=2000 kg,B的质量m2=6000 kg。求汽车与拖车的连接处沿运动方向的相互作用力。取重力加速度g=10 m/s2。
据报道,最近已研制出一种可以投入使用的电磁轨道炮,其原理如图所示。炮弹(可视为长方形导体)置于两固定的平行导轨之间,并与轨道壁密接。开始时炮弹在轨道的一端,通以电流后炮弹会被磁力加速,最后从位于导轨另一端的出口高速射出。设两导轨之间的距离w=0.10 m,导轨长L=5.0 m,炮弹质量m=0.30 kg。导轨上的电流I的方向如图中箭头所示。可认为,炮弹在轨道内运动时,它所在处磁场的磁感应强度始终为B=2.0 T,方向垂直于纸面向里。若炮弹出口速度为v=2.0×103 m/s,求通过导轨的电流I。忽略摩擦力与重力的影响。