如图所示,两根平行金属导轨与水平面间的夹角α=30°,导轨间距为l = 0.50m,金属杆ab、cd的质量均为m=1.0kg,电阻均为r = 0.10Ω,垂直于导轨水平放置.整个装置处于匀强磁场中,磁场方向垂直于轨道平面向上,磁感应强度B = 2.0T.用平行于导轨方向的拉力拉着ab杆沿轨道以某一速度匀速上升时,cd杆恰好保持静止.不计导轨的电阻和摩擦,重力加速度g =10m/s2.求: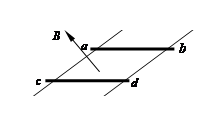
(1)回路中感应电流I的大小.
(2)拉力做功的功率.
如图甲所示,在以O为坐标原点的 平面内,存在着范围足够大的电场和磁场。一个质量
平面内,存在着范围足够大的电场和磁场。一个质量 ,带电量
,带电量 的带电小球在0时刻以
的带电小球在0时刻以 的速度从O点沿
的速度从O点沿 方向(水平向右)射入该空间,在该空间
方向(水平向右)射入该空间,在该空间 同时加上如图乙所示的电场和磁场,其中电场沿
同时加上如图乙所示的电场和磁场,其中电场沿 方向(竖直向上),场强大小
方向(竖直向上),场强大小 。磁场垂直于
。磁场垂直于 平面向外,磁感应强度大小
平面向外,磁感应强度大小 。取当地的重力加速度
。取当地的重力加速度 ,不计空气阻力,计算结果中可以保留根式或
,不计空气阻力,计算结果中可以保留根式或 。试求:
。试求:

(1) 末小球速度的大小。
末小球速度的大小。
(2)在给定的 坐标系中,大体画出小球在0~
坐标系中,大体画出小球在0~ 内运动轨迹的示意图。
内运动轨迹的示意图。
(3) 末小球的位置坐标。
末小球的位置坐标。
2009年中国女子冰壶队首次获得了世界锦标赛冠军,这引起了人们对冰壶运动的关注。冰壶由花岗岩凿磨制成,底面积约为0. 018 m2,质量约为20kg。比赛时,冰壶由运动员推出后在一个非常平整的冰道上滑行,如图甲所示。冰壶在水平冰面上的一次滑行可简化为如图乙所示的过程:运动员将静止于O点的冰壶(视为质点)沿直线 以恒力
以恒力 推到距O点
推到距O点 m的A点放手,此后冰壶沿
m的A点放手,此后冰壶沿 滑行,最后静止于C点。已知冰面与冰壶间的动摩擦因数
滑行,最后静止于C点。已知冰面与冰壶间的动摩擦因数 ,
, ,取当地的重力加速度
,取当地的重力加速度 。试求:
。试求:
(1)冰壶在A点速度的大小。
(2)运动员以恒力推冰壶的过程中力 做功的平均功率。
做功的平均功率。
(3)若运动员在冰壶行进前方的冰道上用冰刷“刷冰”,使冰转化成薄薄的一层水,从距A点 远的B点开始,将
远的B点开始,将 段冰面与冰壶间的动摩擦因数减小为0.8
段冰面与冰壶间的动摩擦因数减小为0.8 ,原来只能滑到C点的冰壶能静止于
,原来只能滑到C点的冰壶能静止于 点,求
点,求 点与
点与 点之间的距离
点之间的距离 为多少?
为多少?
如图所示,在倾角θ=30º的斜面上放置一段凹槽B,B与斜面间的动摩擦因数μ=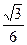 ,槽内靠近右侧壁处有一小球A,它到凹槽内左壁侧的距离d=0.10m.A、B的质量都为m=2.0kg,B与斜面间的最大静摩擦力可认为等于滑动摩擦力,不计A、B之间
,槽内靠近右侧壁处有一小球A,它到凹槽内左壁侧的距离d=0.10m.A、B的质量都为m=2.0kg,B与斜面间的最大静摩擦力可认为等于滑动摩擦力,不计A、B之间 的摩擦,斜面足够长.现同时由静止释放A、B,经过一段时间,A与B的侧壁发生碰撞,碰撞过程不损失机械能,碰撞时间极短.取重力加速度g=10m/s2.求:
的摩擦,斜面足够长.现同时由静止释放A、B,经过一段时间,A与B的侧壁发生碰撞,碰撞过程不损失机械能,碰撞时间极短.取重力加速度g=10m/s2.求:
(1)A与B的左侧壁第一次发生碰撞后瞬间A、B的速度.
(2)在A与B的左侧壁发生第一次碰撞后到第二次碰撞前的这段时间内,A与B的左侧壁的距离最大可达到多少?
足够长的光滑平行金属导轨 和
和 水平放置,在其左端固定一个倾角为
水平放置,在其左端固定一个倾角为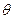 的光滑金属导轨,导轨相距均为
的光滑金属导轨,导轨相距均为 ,在水平导轨和倾斜导轨上,各有一根与导轨垂直的金属杆,两金属杆与水平导轨、倾斜导轨形成—闭合回路。两金属杆质量均为
,在水平导轨和倾斜导轨上,各有一根与导轨垂直的金属杆,两金属杆与水平导轨、倾斜导轨形成—闭合回路。两金属杆质量均为 、电阻均为
、电阻均为 ,其余电阻不计,杆
,其余电阻不计,杆 被销钉固定在倾斜导轨某处。整个装置处于匀强磁场中,磁感应强度为
被销钉固定在倾斜导轨某处。整个装置处于匀强磁场中,磁感应强度为 ,方向竖直向上。当用水平向右、大小
,方向竖直向上。当用水平向右、大小 的恒力拉杆
的恒力拉杆 ,使其达到最大速度时,立即撤去销钉,发现杆
,使其达到最大速度时,立即撤去销钉,发现杆 恰好能在原处仍然保持静止。(重力加速度为
恰好能在原处仍然保持静止。(重力加速度为 )
)
(1)求杆 运动中的最大速度
运动中的最大速度 。
。
(2)求倾斜导轨的倾角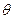 。
。
(3)若杆 加速过程中发生的位移为
加速过程中发生的位移为 ,则杆
,则杆 加速过程中,求杆
加速过程中,求杆 上产生的热量
上产生的热量 。
。
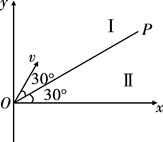
如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为 ,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成
,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成 角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
(1)区域II中磁场的磁感应强度大小;
(2)Q点的坐标。