某校举行托乒乓球跑步比赛,赛道为水平直道,比赛距离为s。比赛时,某同学将球置于球拍中心,以大小为a的加速度从静止开始做匀加速直线运动,当速度达到v0时,再以v0做匀速直线运动跑至终点.整个过程中球一直保持在球拍中心不动.比赛中,该同学在匀速直线运动阶段保持球拍的倾角为θ0,如图所示,设球在运动中受到的空气阻力大小与其速度大小成正比,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g.
(1)求空气阻力大小与球速大小的比值k;
(2)求在加速跑阶段球拍倾角θ随速度v变化的关系式;
(3)整个匀速跑阶段,若该同学速度仍为v0,而球拍的倾角比θ0大了β并保持不变,不计球在球拍上的移动引起的空气阻力变化,为保证到达终点前球不从球拍上距离中心为r的下边沿掉落,求β应满足的条件.
从10 m高空由静止下落的水滴,在下落过程中,水滴重力势能的40%转化为水的内能,使水的温度升高,则水滴落下后温度升高多少?〔水的比热容c=4.2×103 J/(kg·℃)〕
质量均为m的三个小球A、B、C依次用长都是l的细绳相连.置于高为h的光滑水平台面上,l>h,如图所示.在平台边缘右上方的轨道恰能使小球无摩擦地通过,A球位于平台的边缘,受到微小的扰动后开始下落,设A、B两球相继落地后均不弹起,求C球刚要离开平台时的速度大小.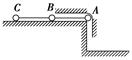
游乐场的过山车的运动过程可以抽象为图4-2-19所示模型.弧形轨道下端与圆轨道相接,使小球从弧形轨道上端A点静止滑下,进入圆轨道后沿圆轨道运动,最后离开.试分析A点离地面的高度h至少要多大,小球才可以顺利通过圆轨道最高点(已知圆轨道的半径为R,不考虑摩擦等阻力).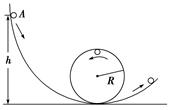
在“验证机械能守恒定律”的实验中,所用电源的频率为50 Hz,某同学选择了一条理想的纸带,用刻度尺测量时各计数点对应刻度尺上的读数如图所示(图中O点是打点计时器打出的第1个点,A、B、C、D、E分别是每打两个点取出的计数点).
根据纸带要求计算:
(1)若重锤的质量为m,则重锤从开始下落到打B点时,减少的重力势能是多少?
(2)重锤下落到打B点时增加的动能有多大?
(3)从(1)(2)数据可得出什么结论?产生误差的主要原因是什么?
如图所示是上海“明珠线”某轻轨车站的设计方案,与站台连接的轨道有一个小坡度,电车进站时要上坡,出站时要下坡,如果坡高2 m,电车到a点的速度是25.2 km/h,此后便切断电动机的电源.如果不考虑电车所受的摩擦力,则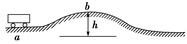
(1)电车到a点电源切断后,能不能冲上站台?
(2)如果能冲上,它到达b点时的速度是多大?(g取10 m/s2)