如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直面内、管口B、C的连线是水平直径,现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R,从小球进入管口开始,整个空间中突然加上一个匀强电场,电场力在竖直向上的分力大小与重力大小相等,结果小球从管口C处脱离圆管后,其运动轨迹最后经过A点,设小球运动过程中带电量没有改变,重力加速度为g,求: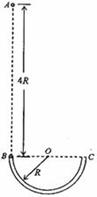
(1)小球到达B点的速度大小;
(2)小球受到的电场力的大小和方向;
(3)小球经过管口C处时对圆管壁的压力。
用细绳将木棒AB的A端吊在天花板上,使木棒在竖直方向上静止不动。在A端正下方有一根半透明的玻璃管CD竖直固定在空中,已知点C端距A端1m,管CD长度为0.8m,把细绳轻轻剪断,测得木棒AB通过玻璃管CD的时间间隔为0. 4s,重力加速度
 ,求木棒AB的长度。
,求木棒AB的长度。
一辆汽车刹车前的速度为126km/h,刹车获得的加速度大小为10 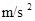 ,求:
,求:
(1)汽车刹车开始后5s内滑行的距离为多少米?
(2)从开始刹车到汽车运动41.25m时所经历的时间?
一个做匀加速直线运动的物体,从某时刻开始观察,2s内的位移为6m,第8s末的速度大小为10m/s,求:
(1)该物体的初速度和加速度各是多大?
(2)该物体在前20s内的位移多大?
(3)速度达到20m/s时的位移是多大?
如图所示,ε1=3V,r1=0.5Ω,R1=R2=5.5Ω,平行板电容器的两板距离d=1cm,当电键K接通时极板中的一个质量m=4×10-3g,电量为q=1.0×10-7C的带电微粒恰好处于静止状态。求:
(1)K断开后,微粒向什么方向运动,加速度多大?
(2)若电容为1000pF,K断开后,有多少电量的电荷流过R2?
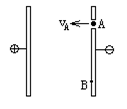
有带电平行板电容器竖直放置,如图9示。板间距d=0.1m、板间电势差U=1000V。现从A处以速度vA=3m/s水平向左射出一带正电的小球(质量m=0.02g、电量为q=10-7C)经过一段时间后发现小球打在A点正下方的B处,(g=10m/s2)求:
(1)分别从水平方向和竖直方向定性分析小球从A到B的过程中,小球的运动情况?
(2)A、B间的距离?(小球由A到B的过程中,不会碰到左极板。)