一个袋子中装有6个红球和4个白球，假设每一个球被摸到的可能性是相等的.
（Ⅰ）从袋子中摸出3个球，求摸出的球为2个红球和1个白球的概率；
（Ⅱ）从袋子中摸出两个球，其中白球的个数为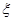
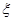，求的分布列和数学期望.
已知函数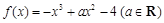
．
(1)若函数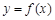
的图象在点P（1，
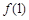）处的切线的倾斜角为
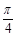，求实数a的值；
(2)设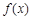
的导函数是
，在 (1) 的条件下，若
，求
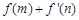的最小值．
(3)若存在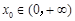
，使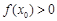
，求a的取值范围．
某工厂在试验阶段大量生产一种零件．这种零件有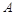
、
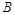两项技术指标需要检测，设各项技术指标达标与否互不影响．若有且仅有一项技术指标达标的概率为
，至少一项技术指标达标的概率为
．按质量检验规定：两项技术指标都达标的零件为合格品．
(1)求一个零件经过检测为合格品的概率是多少？
(2)任意依次抽出5个零件进行检测，求其中至多3个零件是合格品的概率是多少？
已知数列{an}有a1 = a，a2 = p（常数p > 0），对任意的正整数n，
，且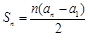
．
(1)求a的值；
(2)试确定数列{an}是否是等差数列，若是，求出其通项公式；若不是，说明理由；
(3)对于数列{bn}，假如存在一个常数b，使得对任意的正整数n都有bn< b，且
，则称b为数列{bn}的“上渐近值”，令
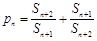，求数列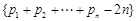
的“上渐近值”．
如右图所示，已知正方形
和矩形
所在的平面互相垂直，
，AF = 1，M是线段
的中点．
(1)求证：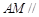
平面
；
(2)求证：
平面
；
(3)求二面角
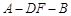的大小．
在一个不透明的纸袋里装有5个大小相同的小球，其中有1个红球和4个黄球，规定每次从袋中任意摸出一球，若摸出的是黄球则不再放回，直到摸出红球为止，求摸球次数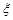
的期望和方差．