某工厂在试验阶段大量生产一种零件.这种零件有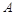 、
、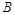 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1) 求一个零件经过检测为合格品的概率是多少?
(2) 任意依次抽出5个零件进行检测,求其中至多3个零件是合格品的概率是多少?
(本小题满分14分)
椭圆 过点P
过点P ,且离心率为
,且离心率为 ,F为椭圆的右焦点,
,F为椭圆的右焦点, 、
、 两点在椭圆
两点在椭圆 上,且
上,且  ,定点
,定点 (-4,0).
(-4,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)当 时 ,问:MN与AF是否垂直;并证明你的结论.
时 ,问:MN与AF是否垂直;并证明你的结论.
(Ⅲ)当 、
、 两点在
两点在 上运动,且
上运动,且 =6
=6 时
时 , 求直线MN的方程.
, 求直线MN的方程.
已知函数 ,
, ,
,
(Ⅰ)当 时,若
时,若 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对 :当
:当 是整数时,存在
是整数时,存在 ,使得
,使得 是
是 的最大值,
的最大值, 是
是 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对 ,试构造一个定义在
,试构造一个定义在 ,且
,且 上的函数
上的函数 ,使当
,使当 时,
时, ,当
,当 时,
时, 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以 为首项的等差数列。
为首项的等差数列。
已知:函数
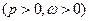 的最大值为
的最大值为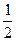 ,最小正周期为
,最小正周期为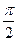 .
.
(Ⅰ)求: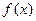 的解析式;
的解析式;
(Ⅱ)若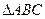 的三条边为
的三条边为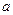 ,
,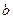 ,
,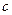 ,满足
,满足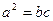 ,
,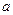 边所对的角为
边所对的角为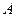 .求:角
.求:角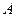 的取值范围及函数
的取值范围及函数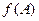 的值域.
的值域.
已知集合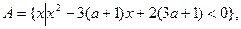
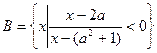 ,
,
(Ⅰ)当 时,求
时,求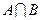 ;
;
(Ⅱ)求使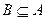 的实数
的实数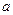 的取值范围。
的取值范围。
已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点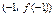 处的切线的斜率是
处的切线的斜率是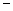 5.
5.
(1)求实数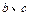 的值;
的值;
(2)求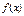 在区间
在区间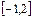 上的最大值;
上的最大值;