(本小题满分12分)已知函数
(1)若数列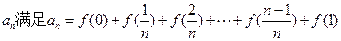 ,求数列
,求数列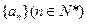 的通项公式;
的通项公式;
(2)若数列 ,则实数k为何值时,不等式
,则实数k为何值时,不等式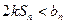 恒成立。
恒成立。
(本小题满分12分)已知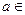 ,函数
,函数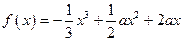 .
.
(Ⅰ)当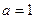 时,求函数f(x)的单调递增区间;
时,求函数f(x)的单调递增区间;
(Ⅱ)若函数f(x)在上单调递减,求的取值范围;
(Ⅲ)若函数f(x)在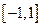 上单调递增,求的取值范围.
上单调递增,求的取值范围.
在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为

(1)求角B;
(2)设 的取值范围。
的取值范围。
(本小题满分12分)已知点列M
 ,M
,M
 ,…,M
,…,M
 ,…,且
,…,且 与
与
 垂直,其中是不等于零的实常数,是正整数,设
垂直,其中是不等于零的实常数,是正整数,设 ,求数列
,求数列 的通项公式,并求其前n项和S
的通项公式,并求其前n项和S 。
。
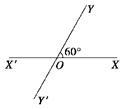
如图所示,有两条相交成60°角的直路XX′和YY′,交点是O,甲、乙分别在OX、OY上,起初甲离O点3 km,乙离O点1 km,后来两人同时用每小时4 km的速度,甲沿XX′方向,乙沿Y′Y的方向步行.
(1)起初,两人的距离是多少?
(2)用t表示t小时后两人的距离;
(3)什么时候两人的距离最短?