已知函数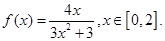
(1)求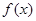 的值域;
的值域;
(2)设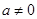 ,函数
,函数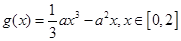 .若对任意
.若对任意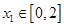 ,总存在
,总存在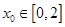 ,使
,使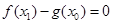 ,求实数
,求实数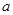 的取值范围.
的取值范围.
一自来水厂拟建一座平面图形为矩形、面积为200平方米的净水处理池,该池的深度为1米,池的四周内壁建造单价为每平方米400元,池底建造单价为每平方米60元,在该水池长边的正中间设置一个隔层,将水池分成左右两个小水池,该隔层建造单价为每平方米100元,池壁厚度忽略不计.
(1)净水池的长度设计为多少米时,可使总造价最低?
(2)如长宽都不能超过14.5米,那么此净水池的长为多少时,可使总造价最低?
如图,ABCD是边长为2的正方形,ABEF是矩形,且二面角C—AB—F是直二面角,AF=1,G是EF的中点.
(1)求证:平面AGC 平面BGC;
平面BGC;
(2)求GB与平面AGC所成角的正弦值.
如图,在正三棱柱ABC—A1B1C1中,底面边长为 ,D为BC中点,M在BB1上,且
,D为BC中点,M在BB1上,且
 .
.
(1)求证: ;
;
(2)求四面体 的体积.
的体积.
如图,在正方体ABCD—A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN//平面AA1B1B.
经过点 作直线l,若直线l与连接
作直线l,若直线l与连接 的线段总有公共点.
的线段总有公共点.
(1)求直线l斜率k的范围;
(2)直线l倾斜角 的范围;
的范围;