已知向量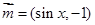 ,向量
,向量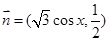 ,函数
,函数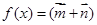 ·
·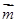 .
.
(1)求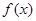 的最小正周期T;
的最小正周期T;
(2)若方程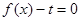 在
在 上有解,求实数
上有解,求实数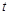 的取值范围.
的取值范围.
已知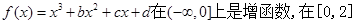 上是减函数,且
上是减函数,且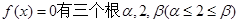 。
。
(1)求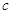 的值,并求出
的值,并求出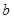 和
和 的取值范围。
的取值范围。
(2)求证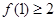 。
。
(3)求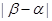 的取值范围,并写出当
的取值范围,并写出当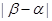 取最小值时的
取最小值时的 的解析式。
的解析式。
设a>0且a≠1, (x≥1)
(x≥1)
(Ⅰ)求函数f(x)的反函数f-1(x)及其定义域;
(Ⅱ)若 ,求a的取值范围。
,求a的取值范围。
设函数 ,已知
,已知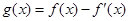 是奇函数。
是奇函数。
(Ⅰ)求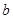 、
、 的值。
的值。
(Ⅱ)求 的单调区间与极值。
的单调区间与极值。
对于定义域为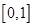 的函数
的函数 ,如果同时满足以下三条:①对任意的
,如果同时满足以下三条:①对任意的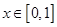 ,总有
,总有 ;②
;② ;③若
;③若 ,都有
,都有 成立,则称函数
成立,则称函数 为理想函数.
为理想函数.
(1) 若函数 为理想函数,求
为理想函数,求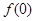 的值;
的值;
(2)判断函数
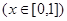 是否为理想函数,并予以证明;
是否为理想函数,并予以证明;
(3) 若函数 为理想函数,
为理想函数, 假定
假定
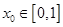 ,使得
,使得 ,且
,且 ,求证:
,求证: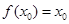 .
.
设数列 的首项为
的首项为 ,前n项和
,前n项和 满足关系式:
满足关系式:
1)求证: 数列 是等比数列;
是等比数列;
2)设数列 的公比为f(t),作数列
的公比为f(t),作数列 ,使得
,使得 ,求:b
,求:b 及
及 ;
;
3)求和 。
。