如图以y轴为边界，右边是一个水平向左的E1=1×104N/C匀强电场，左边是一个与水平方向成45°斜向上的E2=
×104N/C匀强电场，现有一个质量为m=1.0g，带电量q=1.0×10－6C小颗粒从坐标为（0.1，0.1）处静止释放。忽略阻力，g=10m/s2。 求
（1）第一次经过y轴时的坐标及时间
（2）第二次经过y轴时的坐标
在真空中存在空间范围足够大的、水平向右的匀强电场。若将一个质量为m、带正电电量q的小球在此电场中由静止释放，小球将沿与竖直方向夹角为
的直线运动。现将该小球从电场中某点以初速度v0竖直向上抛出，求运动过程中（取sin37°=0.6，cos37°=0.8）小球受到的电场力的大小及方向；
小球运动的抛出点至最高点之间的电势差U．
如图所示，正方形ABCD处在一个匀强电场中，电场线与正方形所在平面平行。已知A、B、C三点的电势依次为UA=6.0V，UB=4.0V，UC=-2.0V．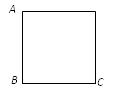
求D点的电势UD．
在图中画出过A点的电场线（要把作图过程画在图上，只画最后结果不能得分）。
一辆汽车在平直公路上做匀变速直线运动，公路边每隔15m有一棵树，如图所示，汽车通过AB两相邻的树用了3s，通过BC两相邻的树用了2s，求汽车运动的加速度和通过树B时的速度为多少?
一架飞机着陆时的速度大小为60m/s，着陆后以6m/s2大小的加速度做匀减速直线运动，求：它着陆后滑行225m时的速度大小；
它着陆后12s内滑行的位移大小。
屋檐定时滴出水滴，当第5滴正欲滴下时，第1滴已刚好到达地面，而第3滴与第2滴正分别位于高1m的窗户的上、下沿，（g=10m/s2）.问：此屋檐离地面多少m？
滴水的时间间隔是多少？