已知函数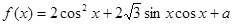 ,且当
,且当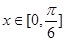 时,
时, 的最小值为2.
的最小值为2.
(1)求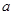 的值,并求
的值,并求 的单调增区间;
的单调增区间;
(2)将函数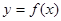 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的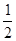 倍,再把所得图象向右平移
倍,再把所得图象向右平移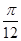 个单位,得到函数
个单位,得到函数 ,求方程
,求方程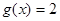 在区间
在区间 上的所有根之和.
上的所有根之和.
如图,四棱锥P-ABCD的底面为正方形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD,
(I) 求证:平面PAD⊥平面PCD
(II)求二面角A-PC-D的余弦值.
某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是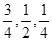 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为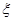 ,求
,求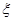 的分布列、数学期望和方差.
的分布列、数学期望和方差.
已知函数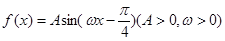 ,
, 的最大值是1且其最小正周期为
的最大值是1且其最小正周期为 .
.
(1)求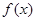 的解析式;
的解析式;
(2)已知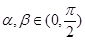 ,且
,且 ,求
,求 的值.
的值.
已知函数 ,其中
,其中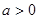 .
.
(1)若对一切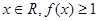 恒成立,求
恒成立,求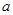 的取值范围;
的取值范围;
(2)在函数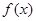 的图像上取定两点
的图像上取定两点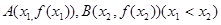 ,记直线
,记直线 的斜率为
的斜率为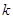 ,证明:存在
,证明:存在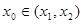 ,使
,使 成立.
成立.
已知函数 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线 垂直。
垂直。
(1)求实数 的值;
的值;
(2)若函数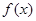 在区间
在区间 上单调递增,求
上单调递增,求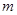 的取值范围.
的取值范围.