如图所示，质量不计、劲度系数为k=600N/m的弹簧一端固定在倾角为37°的光滑斜面底端，另一端拴住质量m1="4" kg的物块P，与P紧靠的是质量m2="8" kg的重物Q，系统处于静止。现给Q施加一个方向沿斜面向上的力F，使它从静止开始沿斜面向上做匀加速运动，已知在前0.2 s时间内，F为变力，0.2 s以后，F为恒力。sin37°=0.6，g取10 m/s2；求：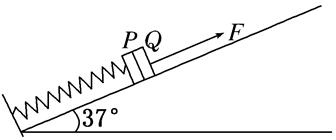
（1）系统静止时，弹簧的形变量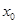
（2）物块Q匀加速运动时的加速度的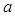
大小
（3）力F的最大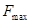值
与最小值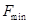
(19分)如图所示，在
的空间中存在匀强电场，场强沿
负方向；在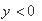
的空间中，存在匀强磁场，磁场方向垂直
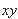平面(纸面)向外。一电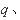量为
质量为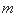
的带正电的运动粒子，经过上
处的点
时速率为
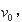方向沿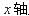
正方向；然后，经过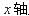上
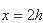处的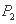
点进入磁场，并经过上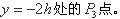
不计粒子重力。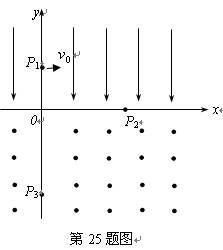
求
(l)电场强度的大小。
(2)粒子到达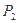
时速度的大小和方向。
(3)磁感应强度的大小。
如图，MNP为竖直面内一固定轨道，其圆弧段MN与水平段NP相切于N、P端固定一竖直挡板。M相对于N的高度为h，NP长度为s。一木块自M端从静止开始沿轨道下滑，与挡板发生一次完全弹性碰撞后停止在水平轨道上某处。若在MN段的摩擦可忽略不计，物块与NP段轨道间的滑动摩擦因数为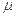
，求物块停止的地方与N点距离的可能值。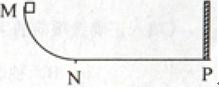
如图所示是质谱仪示意图，图中离子源S产生电荷量为q的离子，经电压为U的电场加速后，由A点垂直射人磁感应强度为B的有界匀强磁场中，经过半个圆周，打在磁场边界底片上的P点，测得PA=d，求离子的质量m。
已知地球半径为R，地球表面的重力加速度为g，地球自转的周期为T，试求地球同步卫星的向心加速度大小。
如图所示，在水平向右的匀强电场中，长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点，平衡时，小球位于B点，此时绳与竖直方向的夹角为θ（θ<45°）。已知重力加速度为g。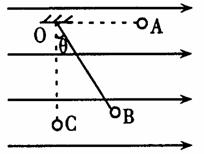
求：
（1）小球静止在B点时受到绳的拉力大小。
（2）若将小球拉到O点等高的A点（此时绳拉直），然后释放小球，当小球运动到最低点C时受到绳的拉力大小。