如图所示，在竖直平面内固定一光滑
圆弧轨道AB，轨道半径为R＝0.4m，轨道最高点A与圆心O等高。有一倾角θ＝30°的斜面，斜面底端C点在圆弧轨道B点正下方、距B点H＝1.5m。圆弧轨道和斜面均处于场强E＝100N/C、竖直向下的匀强电场中。现将一个质量为m=0.02kg、带电量为
的带电小球从A点静止释放，小球通过B点离开圆弧轨道沿水平方向飞出，当小球运动到斜面上D点时速度方向恰与斜面垂直，并刚好与一个以一定初速度从斜面底端上滑的物块相遇。若物块与斜面间动摩擦因数
，空气阻力不计，g取10m/s2，小球和物块都可视为质点。求：
（1）小球经过B点时对轨道的压力NB；
（2）B、D两点间电势差UBD；
（3）物块上滑初速度v0满足的条件。
如图所示，在x轴
上方有垂直于xy平面向里的匀强磁场，磁感应强度为B.在x轴下方有沿y轴负方向的匀强电场，场强为E，一质量为m，电荷量为-q的粒子从坐标原点O沿着y轴正方向射出，射出之后，第五次到达x轴时，它与点O的距离为L，重力不计，求：
（1）粒子运动的轨道半径R
（2）粒子射出的速度v
（3）运动的总路程s.
在与水平面成60°角的光滑金属导轨间连一电源，在相距为1m的平行导轨上放一质量为0.3kg的金属棒ab，通以3A的由b向a的电流，磁场方向竖直向上，这时棒恰好静止．求：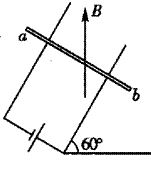
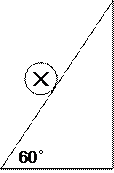
（1）磁感应强度B
（2）棒对导轨的压力大小．(g取10m／s2)
在一次抗洪救灾工作中，一架直升飞机A用长为H=50m悬索（重力忽略不计）系住一质量为m=50kg的被困人员B，直升机A和被困人员B以v0=10m/s的速度一起沿水平方向匀速运动，如图12甲所示。某时刻开始收悬索将人吊起。在t=5s的时间内，A、B之间的竖直距离以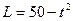
（单位：m）的规律变化，取g=10m/s2。求：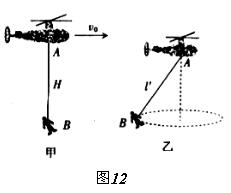
（1）这段时间内悬索对人的拉力大小。
（2）在5s末人的速度大小及该5s内人的位移大小。
（3）直升机在t=5s时停止收悬索，但发现仍然未脱离洪水围困区，为将被困人员B尽快运送到安全处，飞机在空中旋转后静止在空中寻找最近的安全目标，致使被困人员B在空中做圆周运动，如图12乙所示。此时悬索与竖直方向成370角，不计空气阻力，求被困人员B做圆周运动的线速度以及悬索对被困人员B的拉力。（
）
如图11所示，从倾角为q=37°的斜面上的A点以速度v0=10m/s
平抛一个小球。小球落在斜面上的B点，求：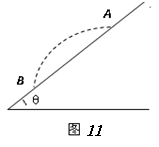
（1）从A点抛出到钢球距离斜面最远时，钢球飞行的时间？
（2）钢球运动过程中距离斜面的最远距离？
（
，
）
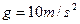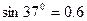如图10所示，射击枪水平放置，射击枪与目标靶中心位于离地面足够高的同一水平线上，枪口与目标靶之间的距离s=100m，子弹射出的水平速度v=200m/s，子弹从枪口射出的瞬间目标靶由静止开始释放，不计空气阻力，取重力加速度g为10 m/s2，求：
（1）从子弹由枪口射出开始计时，经多长时间子弹击中目标靶？
（2）目标靶由静止开始释放到被子弹击中，下落的距离h为多少？