(9分) 在静电场中,将一电量q= -1.5×10―6C的电荷从A点移到B点,电场力做功为3×10-4J。如果将该电荷从C点移到A点,克服电场力做功1.5×10-4J。
(1)求AB两点间的电势差、AC两点间的电势差
(2)若将此电荷从A点移动到无穷远处,克服电场力做功为6×10-4J,求电荷在A点的电势。(设无穷远电势为零)
如图所示,光滑平行的水平金属导轨MN、PQ相距d,在M点和P点间接一个阻值为R的电阻,在两导轨间OO1O1′O′矩形区域内有垂直导轨平面竖直向下、宽为l的匀强磁场,磁感应强度大小为B;质量为m,电阻为r的导体棒ab,垂直搁在导轨上,与磁场左边界相距l0,现用一大小为F、水平向右的恒力拉ab棒,使它由静止开始运动,棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好的接触,导轨电阻不计).求: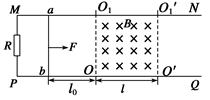
⑴棒ab在离开磁场右边界时的速度;
⑵棒ab通过磁场区域的过程中通过电阻R的电荷量.
某一空间飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰好沿与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,求: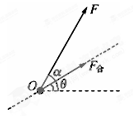
(1)t时刻飞行器的速率;
(2)整个过程中飞行器离地的最大高度.
如图(a)所示,“ ”型木块放在光滑水平地面上,木块水平表面AB粗糙, BC表面光滑且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
”型木块放在光滑水平地面上,木块水平表面AB粗糙, BC表面光滑且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
(1)斜面BC的长度;
(2)木块AB表面的摩擦因数.
研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间)0=0.4s,但饮酒会导致反应时间延长,在某次试验中,志愿者少量饮酒后驾车以v1=72km/h的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m,减速过程中汽车位移x与速度v的关系曲线如同乙所示,此过程可视为匀变速直线运动,取重力加速度的大小g=10m/s2,求: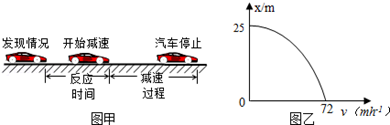
(1)减速过程汽车加速度的大小及所用时间;
(2)饮酒使志愿者反应时间比一般人增加了多少;
(3)减速过程汽车对志愿者作用力的大小与志愿者重力大小的比值.
在一次执行特殊任务的过程中,飞行员在距地面80m高的水平面上做匀加速直线运动的某波音轻型飞机上依次抛出a、b、c三个物体,抛出的时间间隔为1s,抛出点a、b与b、c间距分别为45m和55m,三个物体分别落在水平地面上的A、B、C三处.求: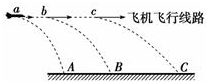
(1)飞机飞行的加速度;
(2)刚抛出b物体时飞机的速度大小;
(3)b、c两物体落地点B、C间的距离.