在物理学中，常常用等效替代、类比、微小量放大等方法来研究问题。如在牛顿发现万有引力定律一百多年后，卡文迪许利用微小量放大法由实验测出了万有引力常量G的数值，图所示是卡文迪许扭秤实验示意图。卡文迪许的实验常被称为是“称量地球质量”的实验，因为由G的数值及其他已知量，就可计算出地球的质量，卡文迪许也因此被誉为第一个称量地球的人。
（1）若在某次实验中，卡文迪许测出质量分别为m1、m2相距为r的两个小球之间引力的大小为F，求万有引力常量G；
（2）若已知地球半径为R，地球表面重力加速度为g，万有引力常量为G，忽略地球自转的影响，请推导出地球质量及地球平均密度的表达式。
一列沿着x轴传播的横波，在t=0时刻的波形如左图所示。左图中x=2cm处的质点P的振动图象如图所示。求：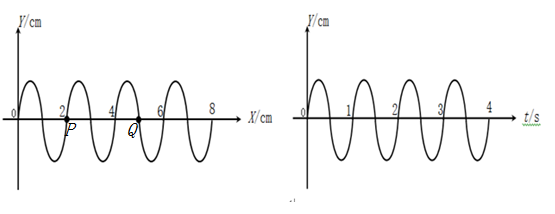
①该波的波速和传播方向；
②从t=0时刻开始质点P出现在波峰的时间；
③从t=0时刻开始，左图中左图中x=5cm处的质点Q第三次出现波峰的时间。
某同学利用DIS实验系统研究一定质量理想气体的状态变化，实验后计算机屏幕显示如图所示的P-V图象．已知在状态A时气体的体积为TA=127°，问：
①气体在状态B和状态C的温度是多少？
②从状态B到状态C这个过程中，会经过一个与状态A温度相同的状态D，则状态D的压强是多少？
③从状态A经状态B到状态C这个过程中，气体对外做功多少？
如图所示，x轴为水平方向，y轴为竖直方向，在第一、三、四象限内有垂直纸面向里的匀强磁场B（图中没画），在x轴上方的与X轴夹角为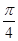
的匀强电强E1，在x轴下方有与竖起直向上的匀强电场E2。一个质量为m、电荷量为q的带正电的小球在第一象限的P（x0，，y0）点，以速度v0竖直向下匀速运动（在第一象限内），当带电小球从第一象限进入第四象限后，第一象限内的磁场消失，小球最终又回到P点。已知：
，
，重力加速度g。求：
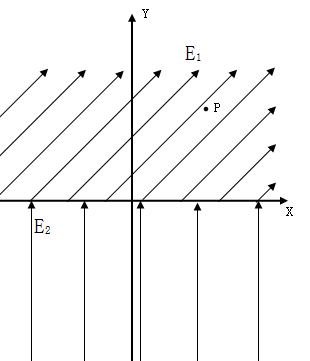
（1）磁感应强度B和电场强度E1；
（2）带电小球的从P点出发到重新回到P点的运动时间和P点的纵坐标y0；
（3）带电小球的从P点出发到重新回到P点的整个过程中电场力做的功和在这个过程中重力做功的最大值。
如图所示，A、B两点在同一水平线上，B点在斜面的延长线上，斜面倾角θ=45°。甲物体在A点以10m/s初速度水平抛出，恰好落在斜面项端，并刚好沿斜面下滑，经过时间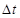
后，乙物体在B点以20m/s初速度水平抛出，正好在斜面上某点到与甲物体相碰。已知：甲物体与斜面的动摩擦因数是
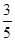。求：
（1）A、B两点间的距离；
（2）乙物体比甲物体后抛的时间。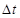
底面光滑的木板B和C长度均为L，小木块A静止于B的右端，C以初速度
水平向右匀速直线运动与B发生正碰并且碰后粘在一起， B、C质量相等均为m，A的质量为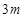
。重力加速度取
。
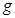（1）求木板B的最大速度；
（2）若要求物块A不会掉在水平面上，则物块与木板间的动摩擦因数μ至少是多大。