如图所示，x轴为水平方向，y轴为竖直方向，在第一、三、四象限内有垂直纸面向里的匀强磁场B（图中没画），在x轴上方的与X轴夹角为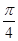
的匀强电强E1，在x轴下方有与竖起直向上的匀强电场E2。一个质量为m、电荷量为q的带正电的小球在第一象限的P（x0，，y0）点，以速度v0竖直向下匀速运动（在第一象限内），当带电小球从第一象限进入第四象限后，第一象限内的磁场消失，小球最终又回到P点。已知：
，
，重力加速度g。求：
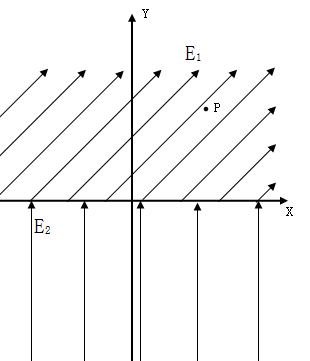
（1）磁感应强度B和电场强度E1；
（2）带电小球的从P点出发到重新回到P点的运动时间和P点的纵坐标y0；
（3）带电小球的从P点出发到重新回到P点的整个过程中电场力做的功和在这个过程中重力做功的最大值。
质量是60kg的人站在升降机中的体重计上（g取10m/s2），求：
(1)升降机匀速上升时体重计的读数；
(2)升降机以4m/s2的加速度匀加速上升时体重计的读数；
(3)当体重计的读数是420N时，判断升降机的运动情况。
从20m高处以15m/s的速度水平抛出一个物体，不计空气阻力，g=10m/s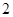
.求：
（1）物体在空中运动的时间多长；
（2）物体落地点离抛出点的水平距离s为多大。
用相同钢珠从斜面上的某点每隔0.1s放下一颗，在连续放下几颗后，对于在斜面上运动的小钢珠摄得如图所示的相片，现测得AB＝15cm，BC=20cm，
试求：
（1）钢珠运动的加速度；
（2）拍摄时B钢珠的速度；
（3）A钢珠上面正在运动的钢珠还有几颗？
如图所示，一个放置在水平地面上的木块，其质量为m=2kg，受到一个斜向下的、与水平方向成30o角的推力F=10N的作用，使木块从静止开始运动，5s后撤去推力。若木块与地面间的动摩擦因数μ=0.1，求木块在地面上运动的总位移。(g=10m/s2,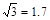
)
一个质量m=3kg的物体放在一长木板上，当木板一端抬起使它与水平方向成θ=30°时，物体正好可以沿板面匀速下滑。当木板水平放置时，用多大的水平拉力才能将物体拉动？（设物体受到的最大静摩擦力等于滑动摩擦力）