如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量为mB的小球连接,另一端与套在光滑直杆上质量mA的小物块连接,已知mA=mB=m,直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=60°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,试求:
(1)小物块能下滑的最大距离;
(2)小物块在下滑距离为L时的速度大小.
如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m。有一质量500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处。(g取l0m/s2)求: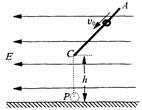
⑴小环离开直杆后运动的加速度大小和方向。
⑵小环从C运动到P过程中的动能增量。
⑶小环在直杆上匀速运动速度的大小v0。
如图,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b。 a球质量为m,静置于地面;b球质量为3m,用手托往,高度为h,此时轻绳刚好拉紧。从静止开始释放b后,a可能达到的最大高度为多少?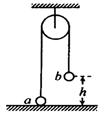
12分)一辆小型载重汽车的质量是3.0t,沿着一条水平公路行驶,行驶过程中牵引力的功率保持不变,汽车所受阻力与汽车对地面的压力成正比。已知牵引力的功率恒为90kW,行驶的最大速度是25m/s。(计算时g取10m/s2)
(1)求汽车在运动过程中受到的阻力是多大。
(2)求当汽车速度为20m/s时的加速度
(3)汽车从静止开始行驶10000m时,速度已达最大,求此过程的时间。
卡车原来以10m/s的速度在平直公路上匀速行驶,因为路口出现红灯,司机从较远的地方开始刹车,使卡车匀减速前进,当车速减到2 m/s时,交通灯转为绿灯,司机当即停止刹车,并且只用了减速过程的一半时间就加速到原来的速度,从刹车开始到恢复原速过程用了12 s。求:
(1)减速与加速过程中的加速度大小。
(2)开始刹车后2s末及10s末的瞬时速度。
一个滑雪人,以2m/s 的初速度从山坡上匀加速滑下,经24s滑到山坡底端,滑到山坡底端的末速度是5.0m/s,求:
(1)下滑的加速度a;
(2)下滑过程中的平均速度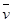 ;
;
(3) 滑雪人下滑的位移。