已知函数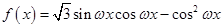 ,其中
,其中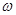 为使
为使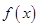 能在
能在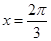 时取得最大值的最小正整数.
时取得最大值的最小正整数.
(1)求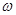 的值;
的值;
(2)设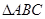 的三边长
的三边长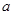 、
、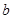 、
、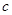 满足
满足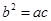 ,且边
,且边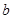 所对的角
所对的角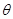 的取值集合为
的取值集合为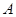 ,当
,当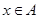 时,求
时,求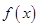 的值域.
的值域.
(本小题12分)已知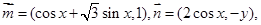 满足
满足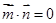 .
.
(1)将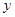 表示为
表示为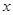 的函数
的函数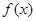 ,并求
,并求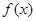 的单调递增区间;
的单调递增区间;
(2)已知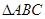 三个内角
三个内角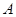 、
、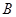 、
、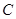 的对边分别为
的对边分别为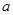 、
、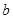 、
、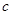 ,若
,若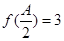 ,且
,且 ,求
,求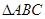 面积的最大值.
面积的最大值.
如图,在正方体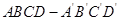 中,点
中,点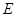 是
是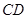 的中点.
的中点.
(1) 求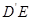 与
与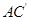 所成的角的余弦值;
所成的角的余弦值;
(2) 求直线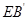 与平面
与平面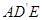 所成的角的余弦值.
所成的角的余弦值.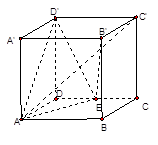
某小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(I)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(II)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数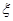 是一个随机变量,求随机变量
是一个随机变量,求随机变量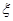 的分布列及数学期望
的分布列及数学期望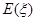 .
.
(选修4—4:坐标系与参数方程)
在极坐标系中,设圆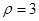 上的点到直线
上的点到直线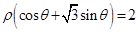 的距离为
的距离为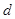 ,求
,求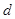 的最大值.
的最大值.
(选修4—2:矩阵与变换)
二阶矩阵M对应的变换将点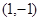 与
与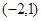 分别变换成点
分别变换成点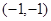 与
与 .
.
(Ⅰ)求矩阵M的逆矩阵 ;
;
(Ⅱ)设直线 在变换M作用下得到了直线
在变换M作用下得到了直线 :
: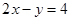 ,求直线
,求直线 的方程.
的方程.