某工厂有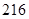 名工人,现接受了生产
名工人,现接受了生产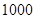 台
台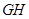 型高科技产品的总任务.已知每台
型高科技产品的总任务.已知每台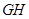 型产品由
型产品由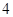 个
个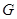 型装置和
型装置和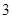 个
个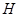 型装置配套组成,每个工人每小时能加工
型装置配套组成,每个工人每小时能加工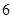 个
个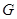 型装置或
型装置或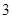 个
个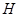 型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工
型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工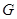 型装置的工人有
型装置的工人有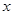 人,他们加工完
人,他们加工完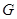 型装置所需时间为
型装置所需时间为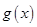 ,其余工人加工完
,其余工人加工完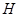 型装置所需时间为
型装置所需时间为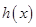 (单位:小时,可不为整数).
(单位:小时,可不为整数).
(1)写出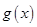 、
、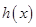 的解析式;
的解析式;
(2)写出这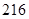 名工人完成总任务的时间
名工人完成总任务的时间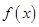 的解析式;
的解析式;
(3)应怎样分组,才能使完成总任务用的时间最少?
(本小题满分12分)等差数列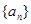 满足:
满足: ,
, ,其中
,其中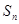 为数列
为数列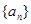 前
前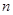 项和.
项和.
(1)求数列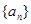 通项公式;
通项公式;
(2)若 ,且
,且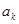 ,
, ,
,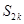 成等比数列,求
成等比数列,求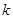 值.
值.
(本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(1)求不等式 的解集;
的解集;
(2)若关于 的不等式
的不等式 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:极坐标于参数方程
已知曲线 (
( 为参数),
为参数), (
( 为参数).
为参数).
(1)化 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若 上的点
上的点 对应的参数为
对应的参数为 ,
, 为
为 上的动点,求
上的动点,求 中点
中点 到直线
到直线 (
( 为参数)距离的最小值.
为参数)距离的最小值.
(本小题满分10分)选修4-1:平面几何选讲
如图,点 在圆
在圆 直径
直径 的延长线上,
的延长线上, 切圆
切圆 于
于 点,
点, 的平分线
的平分线 交
交 于点
于点 ,交
,交 于
于 点.
点.
(1)求 的度数;
的度数;
(2)若 ,求
,求 .
.
(本小题满分12分)已知函数 ,
, .
.
(1)证明: ;
;
(2)若 在
在 恒成立,求
恒成立,求 的最小值.
的最小值.