已知椭圆 、抛物线
、抛物线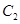 的焦点均在
的焦点均在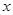 轴上,
轴上, 的中心和
的中心和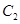 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录如下:
,从每条曲线上取两个点,将其坐标记录如下: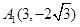 、
、 、
、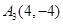 、
、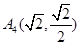 .
.
(1)经判断点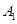 ,
,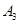 在抛物线
在抛物线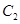 上,试求出
上,试求出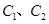 的标准方程;
的标准方程;
(2)求抛物线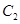 的焦点
的焦点 的坐标并求出椭圆
的坐标并求出椭圆 的离心率;
的离心率;
(3)过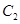 的焦点
的焦点 直线与椭圆
直线与椭圆 交不同两点
交不同两点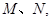 且满足
且满足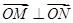 ,试求出直线的方程.
,试求出直线的方程.
如图,在四棱锥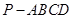 中,底面
中,底面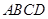 是边长为1的菱形,
是边长为1的菱形,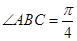 ,
,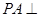 底面
底面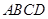 ,
,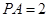 ,
, 为
为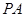 的中点,
的中点,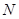 为
为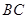 的中点,
的中点,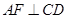 于
于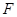 ,如图建立空间直角坐标系.
,如图建立空间直角坐标系.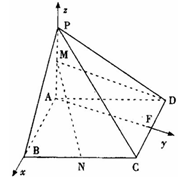
(1)求出平面 的一个法向量并证明
的一个法向量并证明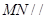 平面
平面 ;
;
(2)求二面角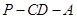 的余弦值.
的余弦值.
数列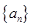 的前
的前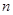 项和为
项和为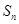 ,
, ,
,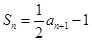
 .
.
(1)求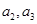 ;
;
(2)求数列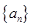 的通项
的通项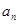 ;
;
(3)求数列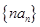 的前
的前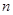 项和
项和 .
.
已知命题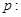 方程
方程 在
在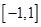 上有解;命题
上有解;命题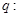 不等式
不等式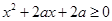 恒成立,若命题“
恒成立,若命题“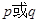 ”是假命题,求
”是假命题,求 的取值范围.
的取值范围.
设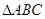 的内角
的内角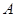 ,
, ,
,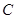 所对的边长分别为
所对的边长分别为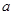 ,
,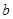 ,
,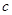 ,且
,且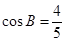 ,
, .
.
(1)当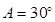 时,求
时,求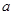 的值;
的值;
(2)当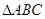 的面积为
的面积为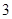 时,求
时,求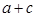 的值.
的值.