如图,AC是圆O的直径,点B在圆O上, ,
,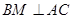 交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,
交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,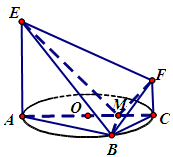
(1)证明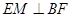 ;
;
(2)(文科)求三棱锥 的体积
的体积
(理科)求平面 和平面
和平面 所成的锐二面角的正切值.
所成的锐二面角的正切值.
要使方程x +px+q = 0的两根a、b满足lg(a+b) = lga+lgb,试确定p和q应满足的关系.
+px+q = 0的两根a、b满足lg(a+b) = lga+lgb,试确定p和q应满足的关系.
已知lgx = a,lgy = b,lgz = c,且有a+b+c = 0,求x ·y
·y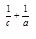 ·x
·x 的值.
的值.
已求函数 的单调区间.
的单调区间.
如图,A,B,C为函数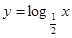 的图象上的三点,它们的横坐标分别是t, t+2, t+4(t
的图象上的三点,它们的横坐标分别是t, t+2, t+4(t 1).
1).
(1)设 ABC的面积为S 求S="f" (t) ;
ABC的面积为S 求S="f" (t) ;
(2)判断函数S="f" (t)的单调性;
(3) 求S="f" (t)的最大值.
现有某种细胞100个,其中有占总数 的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过
的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过 个?(参考数据:
个?(参考数据: )
)