某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日 期 |
4月1日 |
4月7日 |
4月15日 |
4月21日 |
4月30日 |
温差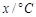 |
10 |
11 |
13 |
12 |
8 |
发芽数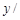 颗 颗 |
23 |
25 |
30 |
26 |
16 |
(Ⅰ)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出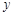 关于
关于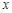 的线性回归方程
的线性回归方程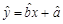 ;
;
(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(Ⅰ)中所得的线性回归方程是否可靠?
(参考公式: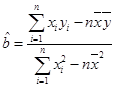
 ,
,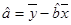 )
)
(参考数据: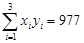 ,
,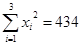 )
)
选修4—1:(本小题满分10分)几何证明选讲
如图,在△ABC中,∠C为钝角,点E,
H分别是边AB上的点,点K和M分别
是边AC和BC上的点,且AH=AC,EB
=BC,AE=AK,BH=BM.
(Ⅰ)求证:E、H、M、K四点共圆;
(Ⅱ)若KE=EH,CE=3,求线段KM的
长.
((本小题满分12分)
已知x>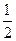 ,函数f(x)=
,函数f(x)= ,h(x)=2e lnx(e为自然常数).
,h(x)=2e lnx(e为自然常数).
(Ⅰ)求证:f(x)≥h(x);
(Ⅱ)若f(x)≥h(x)且g(x)≤h(x)恒成立,则称函数h(x)的图象为函数f(x),g(x)的“边界”.已知函数g(x)=-4 +px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.
+px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.
((本小题满分12分)
在平面直角坐标系xOy中,点P(x,y)为动点,已知点A(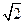 ,0),B(-
,0),B(-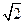 ,0),直线PA与PB的斜率之积为定值-
,0),直线PA与PB的斜率之积为定值-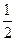 .
.
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,求直线l的方程.
(本小题满分12分)
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
(Ⅰ)求三棱锥C-A1B1C1的体积V;
(Ⅱ)求直线BD1与平面ADB1所成角的正弦值;
(Ⅲ)若棱AA1上存在一点P,使得 =λ
=λ ,
,
当二面角A-B1C1-P的大小为30°时,求实
数λ的值.
(本小题满分12分)
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| 60分以下 |
61-70分 |
71-80分 |
81-90分 |
91-100分 |
|
| 甲班(人数) |
3 |
6 |
11 |
18 |
12 |
| 乙班(人数) |
4 |
8 |
13 |
15 |
10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(Ⅰ)试分别估计两个班级的优秀率;
(Ⅱ)由以上统计数据填写下面2×2列联表,并问是否有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助.
| 优秀人数 |
非优秀人数 |
合计 |
|
| 甲班 |
|||
| 乙班 |
|||
| 合计 |