已知函数 ,
, ,其中
,其中 为常数,
为常数, ,函数
,函数 和
和 的图像在它们与坐标轴交点处的切线分别为
的图像在它们与坐标轴交点处的切线分别为 、
、 ,且
,且 .
.
(1)求常数 的值及
的值及 、
、 的方程;
的方程;
(2)求证:对于函数 和
和 公共定义域内的任意实数
公共定义域内的任意实数 ,有
,有 ;
;
(3)若存在 使不等式
使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.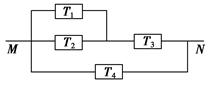
(1)求p;
(2)求电流能在M与N之间通过的概率.
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”,则该课程考核“合格”,若甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7,在实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响.
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三个人该课程考核都合格的概率(结果保留三位小数).
设甲、乙、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.三人各向目标射击一次,求至少有一人命中目标的概率及恰有两人命中目标的概率.
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?
抛掷红、蓝两颗骰子,设事件A为“蓝色骰子的点数为3或6”,事件B为“两颗骰子的点数之和大于8”.
(1)求P(A),P(B),P(AB);
(2)当已知蓝色骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.