如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=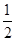 ,AD=1.
,AD=1.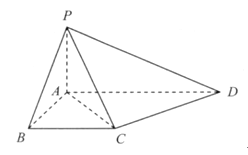
(I)求证:CD⊥平面PAC;
(II)侧棱PA上是否存在点E,使得BE∥平面PCD?若存在,指出点E的位置,并证明,若不存在,请说明理由.
已知函数 ,
, 图象与x轴交点中,相邻两个交点之间的距离为
图象与x轴交点中,相邻两个交点之间的距离为 ,且图象最低点
,且图象最低点
(1)求 解析式
解析式
(2)将 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到 ,求
,求 的单调递减区间
的单调递减区间
函数 函数最大值为1,最小值为
函数最大值为1,最小值为 ,求
,求
某班50名学生在一次百米测试中,成绩介于13秒与18秒之间。将测试结果分成五组,按上述分组方法得到如下频率分布直方图
(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数
(2) 表示该班两位同学百米测试成绩且
表示该班两位同学百米测试成绩且 ,求
,求 的概率
的概率
甲乙两名自行车赛手在相同条件下进行了6次测试,测得最大速度 数据如下:
数据如下:
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
请解答:(1)画茎叶图
(2)求甲乙两组数据的中位数、平均数和标准差并判断谁参加比赛更合适
已知
(1)化简
(2)若 是第三象限角,且
是第三象限角,且 ,求
,求 的值
的值