已知曲线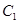 的参数方程为
的参数方程为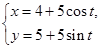 (
(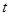 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线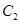 的极坐标方程为
的极坐标方程为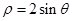 .
.
(Ⅰ)把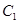 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(Ⅱ)求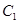 与
与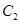 交点的极坐标(
交点的极坐标( ).
).
(本小题满分14分)2008年奥运会在中国举行,某商场预计2008年从1日起前 个月,顾客对某种奥运商品的需求总量
个月,顾客对某种奥运商品的需求总量 件与月份
件与月份 的近似关系是
的近似关系是 且
且 ,该商品的进价
,该商品的进价 元与月份
元与月份 的近似关系是
的近似关系是 且
且 .
.
(1)写出今年第 月的需求量
月的需求量 件与月份
件与月份 的函数关系式;
的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,则此商场
今年销售该商品的月利润预计最大是多少元?
(本小题满分14分)设椭圆
 的左焦点为
的左焦点为 ,上顶点为
,上顶点为 ,过点
,过点 与
与 垂直的直线分别交椭圆
垂直的直线分别交椭圆 与
与 轴正半轴于点
轴正半轴于点 ,且
,且 . ⑴求椭圆
. ⑴求椭圆 的离心率;⑵若过
的离心率;⑵若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线
 相切,求椭圆
相切,求椭圆 的方程.
的方程. 
(本小题满分13分)如图,已知三棱柱 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由 沿棱柱侧面经过棱
沿棱柱侧面经过棱 到点
到点 的最短路线长为
的最短路线长为 ,设这条最短路线与
,设这条最短路线与 的交点为
的交点为 .
.
(1)求三棱柱 的体积;
的体积;
(2)在面 内是否存在过
内是否存在过 的直线与面
的直线与面 平行?证明你的判断;
平行?证明你的判断;
(3)证明:平面 ⊥平面
⊥平面 .
.
(本小题满分13分)某购物广场拟在五一节举行抽奖活动,规则是:从装有编号为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求 的值;(2)若
的值;(2)若 ,且
,且 ,求
,求 的值.
的值.