设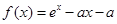 .
.
(Ⅰ)若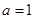 ,求
,求 的单调区间;
的单调区间;
(Ⅱ) 若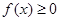 对一切
对一切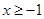 恒成立,求
恒成立,求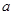 的取值范围.
的取值范围.
(本小题满分12分)已知函数 ,且函数
,且函数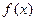 的最小正周期为
的最小正周期为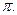
(1)若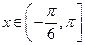 ,求函数
,求函数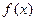 的单调递减区间;
的单调递减区间;
(2)将函数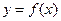 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的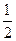 ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数
个单位,得到函数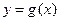 的图象,求函数
的图象,求函数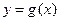 在区间
在区间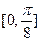 上的最小值。
上的最小值。
(本小题满分12分)
数列 的前n项和为
的前n项和为 ,若
,若
(1)求
(2)是否存在等比数列 满足
满足 若存在,则求出数列
若存在,则求出数列 的通项公式;若不存在,则说明理由。
的通项公式;若不存在,则说明理由。
(本小题满分10分)在锐角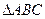 中,A、B、C三内角所对的边分别为a、b、c,
中,A、B、C三内角所对的边分别为a、b、c,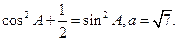
(1)若b=3,求c;
(2)求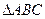 的面积的最大值。
的面积的最大值。
定义在R上的增函数y=f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y).
(Ⅰ)求f (0)
(0)
(Ⅱ)求证f(x)为奇函数;
(Ⅲ)若f(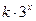 )+f(3
)+f(3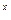 -9
-9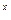 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
设二次函数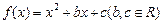 ,已知不论
,已知不论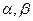 为何实数恒有
为何实数恒有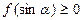 ,
,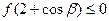
(1)求证: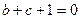 ;
;
( 2)求证:
2)求证: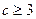 ;
;
(3)若函数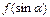 的最大值为8,求
的最大值为8,求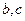 值.
值.