已知等比数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)在 与
与 之间插入
之间插入 个数连同
个数连同 与
与 按原顺序组成一个公差为
按原顺序组成一个公差为 (
( )的等差数列.
)的等差数列.
①设 ,求数列
,求数列 的前
的前 和
和 ;
;
②在数列 中是否存在三项
中是否存在三项 (其中
(其中 成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
设函数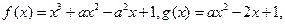 其中实数
其中实数 .
.
(3)若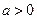 ,求函数
,求函数 的单调区间;
的单调区间;
(4)若 与
与 在区间
在区间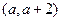 内均为增函数,求
内均为增函数,求
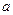 的取值范围.
的取值范围.

如图,已知点 ,且
,且 的内切圆方程为
的内切圆方程为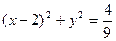 .
.
(1)求经过 三点的椭圆标准方程;
三点的椭圆标准方程;
(2)过椭圆上的点 作圆的切线,求切线长最短时的点
作圆的切线,求切线长最短时的点 的坐标和切线长。
的坐标和切线长。

如图,在四棱锥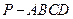 中,
中,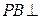 平面
平面 ,
, 底面
底面 是一个直角梯形,
是一个直角梯形,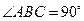 ,
, 。
。
(1)若 为
为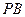 的中点,证明:直线
的中点,证明:直线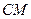 ∥平面
∥平面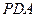 ;
;
(2)求二面角 的余弦值。
的余弦值。
在某电视节目的一次有奖竞猜活动中,主持人准备了A、B两个相互独立的问题,并且宣布:幸运观众答对问题A可获资金1000元,答对问题B可获得奖金2000元,先回答哪个题由观众自由选择,但只有第一个问题答对,才能再答第二题,否则终止答题。若你被选为幸运观众,且假设你答对问题A、B的概率分别为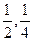 。
。
(1)记先回答问题A获得的奖金数为随机变量 ,求
,求 的分布列及期望。
的分布列及期望。
(2)你觉得应先回答哪个问题才能使你更多的奖金?请说明理由。

(本小题满分12分)一个四棱锥的直观图和三视图如图所示:
|
 ⊥
⊥ ;
;
 的中点 ,证明:直线
的中点 ,证明:直线 ∥平面
∥平面 ;
;

 ,求三棱锥A-PDC的体积.
,求三棱锥A-PDC的体积.