若椭圆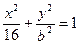 过点(-2,
过点(-2,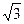 ),则其焦距为()
),则其焦距为()
A.2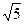 |
B.2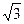 |
C.4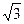 |
D.4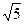 |
已知椭圆的焦点为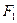 (-1,0)和
(-1,0)和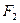 (1,0),P是椭圆上的一点,且
(1,0),P是椭圆上的一点,且 是
是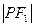 与
与 的等差中项,则该椭圆的方程为()
的等差中项,则该椭圆的方程为()
A.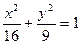 |
B.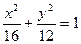 |
C. |
D. |
已知坐标满足方程 的点都在曲线
的点都在曲线 上,那么()
上,那么()
A. 上的点的坐标都适合方程 上的点的坐标都适合方程 ; ; |
B.凡坐标不适合 的点都不在 的点都不在 上; 上; |
C.不在 上的点的坐标必不适合 上的点的坐标必不适合 ; ; |
D.不在 上的点的坐标有些适合 上的点的坐标有些适合 ; ; |
已知点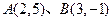 ,则线段AB的方程为()
,则线段AB的方程为()
A.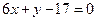 |
B.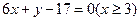 |
C.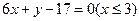 |
D.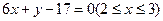 |
函数f(x)的定义域为R,且x≠1,已知f(x+1)为奇函数,当x<1时,f(x)=2x2–x+1,那么当x>1时,f(x)的递减区间是( )
A.[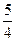 ,+∞ ,+∞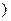 |
B.(1,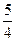 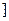 |
C.[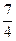 ,+∞ ,+∞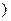 |
D. (1,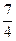 ] ] |