已知抛物线 与双曲线
与双曲线 有公共焦点
有公共焦点 ,点
,点 是曲线
是曲线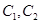 在第一象限的交点,且
在第一象限的交点,且 .
.
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)以双曲线 的另一焦点
的另一焦点 为圆心的圆
为圆心的圆 与直线
与直线 相切,圆
相切,圆 :
: .过点
.过点 作互相垂直且分别与圆
作互相垂直且分别与圆 、圆
、圆 相交的直线
相交的直线 和
和 ,设
,设 被圆
被圆 截得的弦长为
截得的弦长为 ,
, 被圆
被圆 截得的弦长为
截得的弦长为 ,问:
,问: 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
已知函数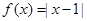
(1)解关于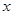 的不等式
的不等式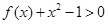
(2)若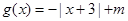 ,
,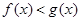 的解集非空,求实数m的取值范围
的解集非空,求实数m的取值范围
在平面直角坐标系xOy中,以坐标原点O为极点x轴的正半轴为极轴建立极坐标系, 曲线C1的极坐标方程为:
(1)求曲线C1的普通方程
(2)曲线C2的方程为 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值
已知函数
(1)当 时,求
时,求 的解集
的解集
(2)若关于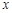 的不等式
的不等式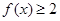 的解集是
的解集是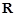 ,求
,求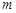 的取值范围
的取值范围
设函数
(Ⅰ)求 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若关于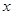 的方程
的方程 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.
(Ⅲ)已知当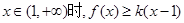 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
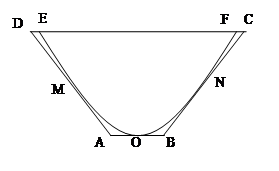
如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米建立适当的直角坐标系,求抛物线方程.
现将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少?