在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的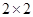 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为 .
.
| |
优秀 |
非优秀 |
合计 |
| 甲班 |
 |
|
|
| 乙班 |
|
 |
|
| 合计 |
|
|
 |
(1)请完成上面的列联表;
(2)根据列联表的数据,能否有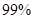 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的 名学生从
名学生从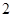 到
到 进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到
进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到 号或
号或 号的概率.
号的概率.
设△ABC的内角A,B,C的对边分别为a,b,c.已知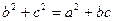 ,求:
,求:
(Ⅰ)A的大小;
(Ⅱ)若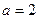 ,求
,求 面积的最大值.
面积的最大值.
如图,在长为52宽为42的大矩形内有一个边长为18的小正方形,现向大矩形内
随机投掷一枚半径为1的圆片,求:
(Ⅰ)圆片落在大矩形内部时,其圆心形成的图形面积;
(Ⅱ)圆片与小正方形及内部有公共点的概率.
执行如图所示的程序框图.
(Ⅰ)当输入n=5时,写出输出的a的值;
(Ⅱ)当输入n=100时,写出输出的T的值.
一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)表中a= ,b = ;
(Ⅱ)画出频率分布直方图;
(Ⅲ)用频率分布直方图,求出总体的众数及平均数的估计值. 频率分布表
频率分布表
| 分组 |
频数 |
频率 |
频率/组距 |
| (10,20] |
2 |
0.10 |
0.010 |
| (20,30] |
3 |
0.15 |
0.015 |
| (30,40] |
4 |
0.20 |
0.020 |
| (40,50] |
a |
b |
0.025 |
| (50,60] |
4 |
0.20 |
0 .020 .020 |
(60, 70] 70] |
2 |
0.10 |
0.010 |
一个口袋内装有大小相同的5 个球,其中3个白球分别记为A1、A2、A3;2个黑
球分别记为B1、B2,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出2球均为白球的概率.