如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连结EC、CD.
(Ⅰ)求证:直线AB是⊙O的切线;
(Ⅱ)若tan∠CED= ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
(本小题满分13分)
从甲、乙两个班中各随机的抽取6名学生,他们的数学成绩如下:
| 甲班 |
76 |
74 |
82 |
96 |
66 |
76 |
| 乙班 |
86 |
84 |
62 |
76 |
78 |
92 |
(I)画出茎叶图并求出甲班学生的数学成绩的中位数;
(II)若不低于80分则表示该生数学成绩为优秀。现从甲、乙两班中各抽出1名学生参加数学兴趣小组,求这两名学生的数学成绩恰好都优秀的概率。
选修4-5:不等式选讲
已知不等式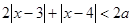
(1)若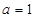 ,求不等式的解集;
,求不等式的解集;
(2)若已知不等式的解集不是空集,求a的取值范围。
选修4-4:坐标系与参数方程
已知曲线 (
( 为参数).
为参数).
(1)将 的方程化为普通方程;
的方程化为普通方程;
(2)若点 是曲线
是曲线 上的动点,求
上的动点,求 的取值范围.
的取值范围.
选修4-1:几何证明选讲
如图, 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的切线,
的切线, 与
与 的延长线交于点
的延长线交于点 ,
, 为切点.若
为切点.若 ,
, ,
, 的平分线
的平分线 与
与 和⊙
和⊙ 分别交于点
分别交于点 、
、 ,求
,求 的值.
的值.
设函数 (
( ),
), .
.
(1) 将函数 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数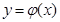 的图象,试写出
的图象,试写出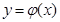 的解析式及值域;
的解析式及值域;
(2) 关于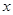 的不等式
的不等式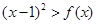 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数 的取值范围;
的取值范围;
(3)对于函数 与
与 定义域上的任意实数
定义域上的任意实数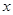 ,若存在常数
,若存在常数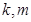 ,使得
,使得 和
和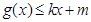 都成立,则称直线
都成立,则称直线 为函数
为函数 与
与 的“分界线”.设
的“分界线”.设 ,
,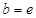 ,试探究
,试探究 与
与 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.