如图所示,机器人海宝按照以下程序运行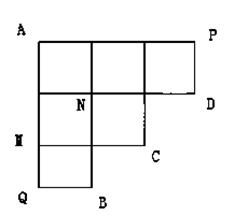
1从A出发到达点B或C或D，到达点B、C、D之一就停止；
②每次只向右或向下按路线运行；
③在每个路口向下的概率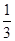
；
④到达P时只向下，到达Q点只向右．
（1）求海宝过点从A经过M到点B的概率，求海宝过点从A经过N到点C的概率；
（2）记海宝到点B、C、D的事件分别记为X=1，X=2，X=3，求随机变量X的分布列及期望．
在△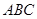
中，
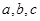是角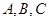
对应的边，向量
,
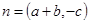，且
．
（1）求角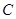
；
（2）函数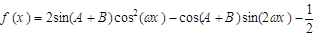
的相邻两个极值的横坐标分别为
、
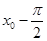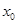，求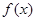
的单调递减区间．
已知关于x的不等式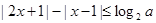
（其中
）．
（1）当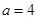
时，求不等式的解集；
（2）若不等式有解，求实数
的取值范围
在平面直角坐标系中，曲线C1的参数方程为
（a＞b＞0，
为参数），以Ο为极点，x轴的正半轴为极轴建立极坐标系，曲线C2是圆心在极轴上且经过极点的圆，已知曲线C1上的点M
对应的参数=
，
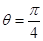与曲线C2交于点D
（1）求曲线C1，C2的方程；
（2）A（ρ1，θ），Β（ρ2，θ+
）是曲线C1上的两点，求
的值。
已知PQ与圆O相切于点A，直线PBC交圆于B、C两点，D是圆上一点，且AB∥CD，DC的延长线交PQ于点Q．
（1）求证：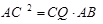
（2）若AQ=2AP，AB=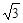
,BP=2，求QD．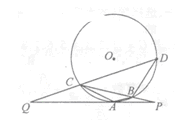
已知函数
是定义在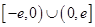
上的奇函数,当
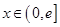时,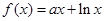 
(其中e是自然界对数的底,
)
（1）求的解析式;
（2）设
，求证：当
时，且
，
恒成立；
（3）是否存在实数a，使得当
时，的最小值是3 ？如果存在，求出实数a的值；如果不存在，请说明理由。