(12分)一个水平方向足够长的传送带以恒定的速度3 m/s沿顺时针方向转动，传送带右端固定着一个光滑曲面，并且与曲面相切，如图所示.小物块从曲面上高为h的P点由静止滑下，滑到传送带上继续向左运动，物块没有从左边滑离传送带。已知传送带与物体之间的动摩擦因数μ=0.2，不计物块滑过曲面与传送带交接处的能量损失，g取10 m/s2。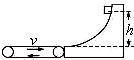
（1）若h1="1.25" m，求物块返回曲面时上升的最大高度。
（2）若h2="0.2" m，求物块返回曲面时上升的最大高度。
如图：直杆上O1O2两点间距为L,细线O1A长为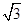
L,O2A长为L,A端小球质量为m，要使两根细线均被拉直，杆应以多大的角速度
转动． 
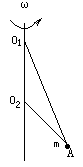
倾角为θ=37。ｏ的斜面上有一个质量为m=1kg的物体，现使斜面在水平方向上以速度v=1m/s向左做匀速直线运动，已知物体与斜面始终保持相对静止，如图所示，试求：
（1）物体通过位移5m的过程中，斜面的支持力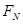
和摩擦力Ff对物体所做的功．
（2）摩擦力的功率．
已知万有引力常量G，地球半径R，月球和地球之间的距离r，同步卫星距地面的高度h，月球绕地球的运转周期T1，地球的自转周期T2，地球表面的重力加速度g.
某同学根据以上条件，提出一种估算地球质量M的方法：
同步卫星绕地球作圆周运动，由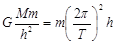
得
⑴请判断上面的结果是否正确，并说明理由.如不正确，请给出正确的解法和结果.
⑵请根据已知条件再提出两种估算地球质量的方法并解得结果。
宇航员的选拔、训练是非常严格的．当航天飞机升空时，宇航员会发生黑视．黑视的原因第一是因为血压降低，导致视网膜缺血，第二是因为脑缺血．为了使宇航员适应飞行要求，在如图8所示的仪器中对宇航员进行训练．宇航员坐在一个在竖直平面内做匀速圆周运动的舱内，若要使宇航员的向心加速度为an＝6g，(已知：R＝20 m，g取10 m/s2)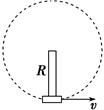
求： （1）仪器旋转的角速度需设定为多少？
（2）宇航员对座椅的压力是自身重力的多少倍？
某同学在某砖墙前的高处水平抛出一石子，石子在空中运动的部分轨迹照片如图7所示。从照片可看出石子恰好垂直打在一倾角为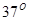
的斜坡上的A点。已知每块砖的平均厚度为20cm，抛出点到A点竖直方向刚好相距100块砖， (sin370="0.6." cos370=0.8)求：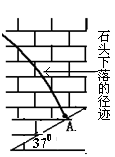
（1）石子在空中运动的时间t；
（2）石子水平抛出的速度v0。