(16分)如图所示,在水平匀速运动的传送带的左端(P点),轻放一质量为m=1kg的物块,物块随传送带运动到A点后抛出,物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑。B、D为圆弧的两端点,其连线水平。已知圆弧半径R=1.0m,圆弧对应的圆心角θ=106º,轨道最低点为C,A点距水平面的高度h=0.80m。(g取10m/s2,
sin53º=0.8,cos53º=0.6)求:

(1)物块离开A点时水平初速度的大小;
(2)物块经过C点时对轨道压力的大小;
(3)设物块与传送带间的动摩擦因数为0.3,传送带的速度为5m/s,求PA间的距离。
如图所示,一个光滑的圆弧形槽半径为R,放在水平地面上,圆弧所对的圆心角小于5°.AD的长为x,今有一小球m1以沿AD方向的初速度v从A点开始运动,要使小球m1可以与固定在D点的小球m2相碰撞,那么小球m1的速度v应满足什么条件?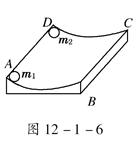
有人利用安装在气球载人舱内的单摆来确定气球的高度.已知该单摆在海平面处的周期是T0.当气球停在某一高度时,测得该单摆周期为T.求该气球此时离海平面的高度h.(把地球看做质量均匀分布的半径为R的球体)
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm.某时刻振子处于B点,经过0.5 s,振子首次到达C点,求:
(1)振动的周期和频率;
(2)振子在5 s内通过的路程及5 s末的位移大小;
(3)振子在B点的加速度大小跟它距O点4 cm处P点的加速度大小的比值.
如图甲所示,在某介质中波源A、B相距d=20 m,t=0时两者开始上下振动,A只振动了半个周期,B连续振动,所形成的波的传播速度都为v=1.0 m/s,开始阶段两波源的振动图象如图乙所示.
(1)定性画出t=14.3 s时A波所达位置一定区域内的实际波形;
(2)求时间t=16 s内从A发出的半波前进过程中所遇到的波峰个数.
如图所示,实线是某时刻的波形图,虚线是0.2 s后的波形图.
(1)若波沿x轴负方向传播,求它传播的可能距离.
(2)若波沿x轴正方向传播,求它的最大周期.
(3)若波速是35 m/s,求波的传播方向.