如图所示，在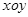
平面直角坐标系中，直线
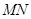与
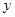轴成30°角，
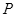点的坐标为（
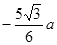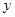，0），在轴与直线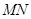之间的区域内，存在垂直于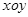平面向里磁感强度为
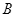的匀强磁场．均匀分布的电子束以相同的速度
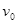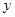从轴上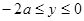
的区间垂直于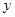轴和磁场方向射入磁场．己知从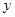轴上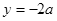
点射入磁场的电子在磁场中的轨迹恰好经过
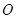点，忽略电子间的相互作用，不计电子的重力．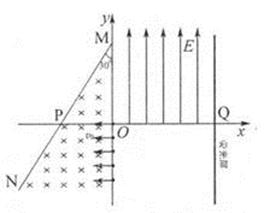
（1）电子的比荷（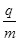
）；
（2）有一电子，经过直线MP飞出磁场时，它的速度方向平行于y轴，求该电子在y轴上的何处进入磁场；（3）若在直角坐标系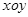的第一象限区域内，加上方向沿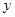轴正方向大小为
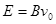的匀强电场，在
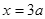处垂直于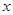
轴放置一平面荧光屏，与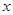轴交点为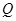
，求：从O点上方最远处进入电场的粒子打在荧光屏上的位置。
如图所示，质量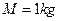
的木板静止在粗糙的水平地面上，木板与地面间的动摩擦因数
，在木板的左端放置一个质量
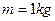、大小可以忽略的铁块，铁块与木板间的动摩擦因数
。最大静摩擦力近似等于滑动摩擦力，重力加速度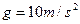
，试求：若木板长
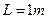，在铁块上加一个水平向右的恒力
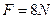，经过多长时间铁块运动到木板的右端？若在铁块上加一个大小从零开始连续增加的水平向右的力
，通过分析和计算后，请在图中画出铁块受到木板的摩擦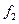力
随拉力大小变化的图像。（设木板足够长）
长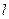
的轻绳，一端固定在O点，另一端系一质量为
小球，在O下方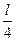
处，将小球水平向右抛出，忽略空气阻力的影响，经过一段时间绳拉直，绳刚拉直时与竖直线夹角
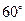，已知绳伸直的一瞬间，沿绳方向的速度瞬间减为零。求：
球水平抛出速度；
球摆到最低点时，绳所受拉力。
“嫦娥奔月”的过程简化为：“嫦娥一号”升空后，首先进入周期为
的近地圆轨道，然后在地面的指令下经过一系列的变轨后最终被月球捕获，在距离月球表面为
的轨道上绕月球做匀速圆周运动。已知地球质量为
，半径为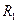
，月球质量为
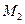，半径为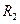
。求：“嫦娥一号”绕月球运动时的周期
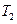（最终结果用题目中的物理量为表示）。
如图所示，一足够长的光滑斜面倾角为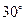
，斜面AB与水平面BC平滑连接。一物体置于水平面上的D点，D点距B点
，物体与水平面的动摩擦因数为
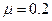。现给物体一个向左初速度
，求物体经多长时间物体经过B点？（重力加速度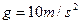
）
如图所示，在区域Ⅰ(0≤x≤d)和区域Ⅱ(d≤x≤2d)内分别存在匀强磁场，磁感应强度大小分别为B和2B，方向相反，且都垂直于Oxy平面．一质量为m、带电荷量q(q＞0)的粒子a于某时刻从y轴上的P点射入区域Ⅰ，其速度方向沿x轴正向．已知a在离开区域Ⅰ时，速度方向与x轴正向的夹角为30°；此时，另一质量和电荷量均与a相同的粒子b也从P点沿x轴正向射入区域Ⅰ，其速度大小是a的；不计重力和两粒子之间的相互作用力．求：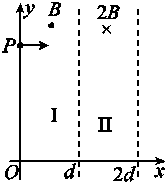
粒子a射入区域Ⅰ时速度的大小；
当a离开区域Ⅱ时，a、b两粒子的y坐标之差．网]