(本题12分)如图所示,一质量为 ,长为
,长为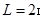 的木板放在水平地面上,已知木板与地面间的动摩擦因数为
的木板放在水平地面上,已知木板与地面间的动摩擦因数为 ,在此木板的右端上还有一质量为
,在此木板的右端上还有一质量为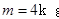 的小物块,且视小物块为质点,木板厚度不计。今对木板突然施加一个
的小物块,且视小物块为质点,木板厚度不计。今对木板突然施加一个 的水平向右的拉力,
的水平向右的拉力, .
.
(1)若木板上表面光滑,则小物块经多长时间将离开木板?
(2)若小物块与木板间的动摩擦因数为 、小物块与地面间的动摩擦因数为
、小物块与地面间的动摩擦因数为 ,小物块相对木板滑动一段时间后离开木板继续在地面上滑行,且对地面的总位移
,小物块相对木板滑动一段时间后离开木板继续在地面上滑行,且对地面的总位移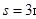 时停止滑行,求
时停止滑行,求 值.
值.
有一根长为2L的轻质细线,它的两端固定在一根长为L的竖直转轴AB上,线上套一个可以自由移动的质量为m的小球.当转轴转动时,小球正好以B为圆心,在水平面内做匀速圆周运动.求细线的张力和小球的线速度.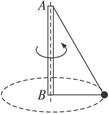
摩托车障碍赛中,运动员在水平路面上遇到一个壕沟,壕沟的尺寸如图6所示,要安全的越过这壕沟,求摩托车的速度v0至少为多大?(空气阻力不计, g=10m/s2)
如图所示,质量为m,带电量为q(q>0)的粒子(重力不计),从离坐标原点为1.5a的 y轴上的P点,以速度大小为v0,方向与y轴正方向成θ=30°射入xoy坐标的第一象限,经过一个在第一象限内,边界形状为等腰梯形方向与xoy坐标面垂直匀强磁场区域,然后沿-x方向经过坐标原点0,进入相互垂直的匀强电场和匀强磁场中,其运动轨迹为虚线所示,该电场强度为E,方向沿-y轴方向,磁感应强度为B,方向垂直坐标面向外。
(1)画出最小的等腰梯形所处的位置和粒子运动轨迹,并求出此时的磁感应强度;
(2)粒子过坐标原点0后的运动可分解为x方向和y方向两分运动组成,已知y方向分运动为简谐运动;求粒子离x轴最远距离。
甲、乙、丙三个物体用不可伸长的轻线通过轻滑轮连接,甲与地面用轻弹簧连接,如图所示。物体乙与物块丙之间的距离和物体丙到地面的距离相等。已知物体乙与物块丙的质量均为m,物体甲的质量大于m,但是小于2m;弹簧的劲度系数为k。物体在运动过程中不会与滑轮相碰,且不计一切阻力,物体碰地后不反弹。
(1)若将乙与丙间的线剪断,甲下降多大距离时它的速度最大?
2)若将弹簧剪断后,要保证物块乙在运动过程中不会着地,求这种情形之下甲物体的质量等于多少? 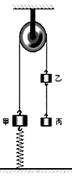
某天,小明在上学途中沿人行道以v1=lm/s速度向一公交车站走去,发现一辆公交车正以v2 =15m/s速度从身旁的平直公路同向驶过,此时他们距车站s =50m。为了乘上该公交车,他加速向前跑去,最大加速度a1=2.5m/s2,能达到的最大速度vm =6m/s。假设公交车在行驶到距车站S0=25m处开始刹车,刚好到车站停下,停车时间t=10s,之后公交车启动向前开去。(不计车长)求:
(1)若公交车刹车过程视为匀减速运动,求其加速度a2的大小;
(2)若小明加速过程视为匀加速运动,通过计算分析他能否乘上该公交车。