如图所示,半径为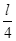 、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、 B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l。当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内)。求:
、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、 B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l。当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内)。求:
(1)竖直杆角速度ω为多大时,小球恰离开竖直杆?
(2)轻绳a的张力Fa与竖直杆转动的角速度ω之间的关系。
如图所示,ABCD为竖立放在场强为E=104 V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与半圆环相切,A为水平轨道上的一点,而且AB=R=0.2m.把一质量m=0.1kg、带电量q=10﹣4C的小球,放在水平轨道的A点由静止开始释放后,在轨道的内侧运动.(g取10m/s2)求: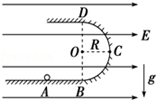
(1)它到达C点时的速度是多大?
(2)若让小球安全通过D点,开始释放点离B点至少多远?
竖直放置的两块足够长的平行金属板间有匀强电场,其电场强度为E,在该匀强电场中,用丝线悬挂质量为m的带电小球,丝线跟竖直方向成θ角时小球恰好平衡,小球与右侧金属板相距d,如图所示,求: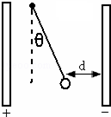
(1)小球带电荷量q是多少?
(2)若剪断丝线,小球碰到金属板需多长时间?
如图所示,在匀强电场中,有A、B两点,它们间距为2cm,两点的连线与场强方向成60°角.将一个电量为﹣2×10﹣5C的电荷由A移到B,其电势能增加了0.1J.则: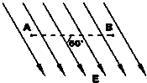
(1)在此过程中,电场力对该电荷做了多少功?
(2)A、B两点的电势差UAB为多少?
(3)匀强电场的场强为多大?
小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动,当球某次运动到最低点时,绳突然断掉。球飞行水平距离d后落地,如图所示,已知握绳的手离地面高度为d,手与球之间的绳长为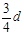 ,重力加速度为g。忽略手的运动半径和空气阻力。试求:
,重力加速度为g。忽略手的运动半径和空气阻力。试求:
⑴球落地时的速度大小v2;
⑵绳子能够承受的最大拉力为多大;
⑶如果不改变手离地面的高度,改变绳子的长度,使小球重复上述的运动。若绳子仍然在小球运动到最低点时断掉,要使小球抛出的水平距离最大,则绳子长度应为多少,小球的最大水平距离为多少?
(14分)如图所示,轻质杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,当球B运动到最低点时,杆对球B的作用力大小为2mg,已知当地重力加速度为g,求此时: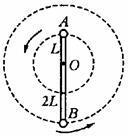
(1)球B转动的角速度大小;
(2)A球对杆的作用力大小以及方向;
(3)在点O处,轻质杆对水平转动轴的作用力大小和方向。