如图所示， A、B、C、D为固定于竖直平面内的闭合绝缘轨道，AB段、CD段均为半径R＝2.5m的半圆，BC、AD段水平，AD ="BC" =" 8" m，B、C之间的区域存在水平向右的有界匀强电场场强E＝ 6 ×105 V/m；质量为m = 4×10－3 kg、带电量q = +1×10－8C的小环套在轨道上，小环与轨道AD段之间存在摩擦且动摩擦因数处处相同，小环与轨道其余部分的摩擦忽略不计，现使小环在D点获得某一初速度沿轨道向左运动，若小环在轨道上可以无限循环运动，且小环每次到达圆弧上的A点时，对圆轨道刚好均无压力．求：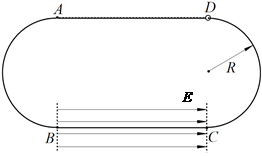
（1）小环通过A点时的速度多大；
（2）小环与AD段间的动摩擦因数μ；
（3）小环运动到D点时的速度多大．
(6分)一物体作匀加速直线运动，在2s内通过的位移为6m，在紧接着的1s内通过的位移也为6m。求物体运动的加速度的大小。
如图所示，以8 m/s速度匀速行驶的汽车即将通过路口，绿灯还
有2 s将熄灭，此时汽车距离停车线17 m．该车加速时最大加速度大小为2 m/s2，减速时最大加速度大小为4 m/s2．此路段允许行驶的最大速度为12．5 m/s，某司机正常反应时间为0．4 s．
问：
（1）这位司机打算加速前进，他能否在绿灯熄灭前通过停车线？
（2）若这位司机酒后驾驶，反应时间变为原来的3倍，分析他是否会闯红灯？
飞机着陆后以6 m/s2大小的加速度做匀减速直线运动，其着陆速度为60 m/s，求：
（1）它着陆后12 s内滑行的位移x；
（2）整个减速过程的平均速度（用两种方法求）；
（3）静止前4 s内飞机滑行的位移x′．
如图所示，一质点沿半径为r="20" cm的圆周自A点出发，逆时针运动2 s，运动圆周到达B点，
求：
（1）质点的位移和路程；
（2）质点的平均速度大小和平均速率．
(19分)如图所示，在
的空间中存在匀强电场，场强沿
负方向；在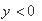
的空间中，存在匀强磁场，磁场方向垂直
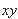平面(纸面)向外。一电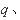量为
质量为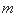
的带正电的运动粒子，经过上
处的点
时速率为
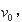方向沿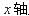
正方向；然后，经过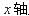上
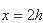处的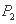
点进入磁场，并经过上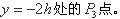
不计粒子重力。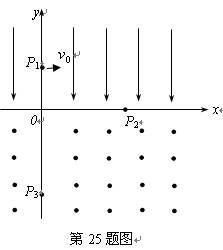
求
(l)电场强度的大小。
(2)粒子到达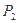
时速度的大小和方向。
(3)磁感应强度的大小。