如图所示,在倾角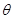 =370的固定斜面底端,放着一个质量为1Kg的物体,现对物体施加平行于斜面向上的恒力F=20N,作用时间
=370的固定斜面底端,放着一个质量为1Kg的物体,现对物体施加平行于斜面向上的恒力F=20N,作用时间 时撤去拉力F,若物体与斜面间的动摩擦因数为μ=0.5,斜面足够长,取
时撤去拉力F,若物体与斜面间的动摩擦因数为μ=0.5,斜面足够长,取 ,sin370=0.6,cos370=0.8。试求:
,sin370=0.6,cos370=0.8。试求:
(1)撤去F时,物体的速度是多少?此过程中F做的功是多少?
(2)物体再返回到斜面低端时的速度是多少?
如图所示,在倾角θ=37°的斜面两端,垂直于斜面方向固定两个弹性板,两板相距L=2m,质量为m=10g,电荷量为q=1×10-7C的物体与斜面间的动摩擦因数为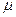 =0.2,物体从斜面中点以大小为10m/s的速度沿斜面开始运动。若物体与弹性板碰撞过程中机械能不损失,电荷量也不变,平行于斜面向上的匀强电场的场强E=2×106N/C,(sin37°=0.6,cos37°=0.8,g取10m/s2).求:
=0.2,物体从斜面中点以大小为10m/s的速度沿斜面开始运动。若物体与弹性板碰撞过程中机械能不损失,电荷量也不变,平行于斜面向上的匀强电场的场强E=2×106N/C,(sin37°=0.6,cos37°=0.8,g取10m/s2).求:
(1)物体在运动过程中受到斜面摩擦力f的大小;
(2)补充完整物体从斜面中点出发第一次到达上端弹性板过程的动能定理表达式,物体的初速度为v,末速度为 (全部用字母表示);
(全部用字母表示); +_______________=____________-____________
+_______________=____________-____________
(3)物体在斜面上运动的总路程.
某校物理兴趣小组举行遥控车比赛,比赛路径如图所示.赛车从A点出发,沿水平桌面运动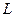 的距离后从B点飞出,过B点时赛车电源自动关闭,越过壕沟后进入光滑的轨道CD,由D点进入半径为R的光滑竖直圆轨道,离开圆轨道后,继续在光滑平直轨道上运动.图中L=4m,h=1.25m,s=1.5m,R=0.32m.已知赛车质量m=0.1kg,赛车通电后受到恒定的牵引力,在水平桌面上受到阻力恒为0.3N,其它过程阻力不计,赛车越过壕沟进入光滑轨道CD时不反弹且无能量损失,(g取10m/s2).求:
的距离后从B点飞出,过B点时赛车电源自动关闭,越过壕沟后进入光滑的轨道CD,由D点进入半径为R的光滑竖直圆轨道,离开圆轨道后,继续在光滑平直轨道上运动.图中L=4m,h=1.25m,s=1.5m,R=0.32m.已知赛车质量m=0.1kg,赛车通电后受到恒定的牵引力,在水平桌面上受到阻力恒为0.3N,其它过程阻力不计,赛车越过壕沟进入光滑轨道CD时不反弹且无能量损失,(g取10m/s2).求:
(1)赛车要安全越过壕沟,在B点的速度至少多大?
(2)赛车要安全通过竖直圆轨道,在D点速度至少多大?
(3)赛车要完成比赛,赛车的牵引力至少多大?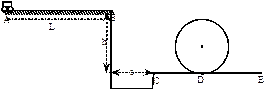
已知万有引力常量G,地球半径R,月球和地球球心之间的距离r,同步卫星距地面的高度h,月球绕地球的运转周期T1,地球的自转周期T2,地球表面的重力加速度为g.某同学根据以上条件,提出一种估算地球质量M的方法:
同步卫星绕地球作圆周运动,由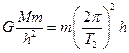 得:
得:
⑴请判断上面的结果是否正确,并说明理由;如不正确,请给出正确的解法和结果;
⑵请根据已知条件再提出两种估算地球质量的方法并解得结果.
4×100m接力赛是奥运会上最为激烈的比赛项目,有甲乙两运动员在训练交接棒的过程中发现,甲短距离加速后能保持9m/s的速度跑完全程.为了确定乙起跑的时机,需在接力区前适当的位置 设置标记,在某次练习中,甲在接力区前s0 处作了标记,当甲跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令时立即起跑(忽略声音传播的时间及人的反应时间),已知接力区的长度为L=20m,设乙起跑后的运动是匀加速运动,试求:
设置标记,在某次练习中,甲在接力区前s0 处作了标记,当甲跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令时立即起跑(忽略声音传播的时间及人的反应时间),已知接力区的长度为L=20m,设乙起跑后的运动是匀加速运动,试求:
(1)若s0 =13.5m,且乙恰好在速度达到与甲相同时被甲追上,完成交接棒,则在完成交接棒时乙离接力区末端的距离为多大?
(2)若s0 =16m,乙的最大速度为8m/s,并能以最大速度跑完全程,要使甲乙能在接力区完成交接棒,则乙在听到口令后加速的加速度最大为多少?(结果保留3位有效数字)
在真空中,氢原子从能级A跃迁到能级B时,辐射出波长为λl的光子;从能级A跃迁到能级C时,辐射出波长为λ2的光子。若λ1>λ2,真空中的光速为c,那么氢原子从能级B跃迁到能级C时是辐射光子还是吸收光子,这个光子的波长为多少?