(如图1)在平面四边形 中,
中,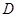 为
为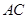 中点,
中点, ,
, ,且
,且 ,现沿
,现沿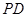 折起使
折起使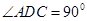 ,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
(1)求三棱锥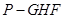 的体积;
的体积;
(2)在线段PC上是否存在一点M,使直线 与直线
与直线 所成角为
所成角为 ?若存在,求出线段的长;若不存在,请说明理由.
?若存在,求出线段的长;若不存在,请说明理由.
已知数列 中,
中, ,
,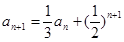 ,(Ⅰ)记
,(Ⅰ)记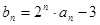 ,证明数列
,证明数列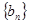 是等比数列;(Ⅱ)求数列
是等比数列;(Ⅱ)求数列 的通项公式.
的通项公式.
在某校举办的元旦有奖知识问答中,甲、乙、丙三人同时回答一道有关环保知识的问题,已知甲回答对这道题的概率是 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 .(Ⅰ)求乙、丙两人各自回答对这道题的概率;(Ⅱ)用
.(Ⅰ)求乙、丙两人各自回答对这道题的概率;(Ⅱ)用 表示回答对该题的人数,求
表示回答对该题的人数,求 的分布列和数学期望E
的分布列和数学期望E .
.
叙述双曲线的定义,并建立适当的直角坐标系推导其标准方程.
已知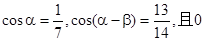 <
< <
< <
<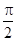 ,
,
(Ⅰ)求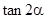 的值.(Ⅱ)求
的值.(Ⅱ)求 .
.
(本小题满分14分)已知函数 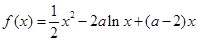 ,
, .
.
(Ⅰ)当 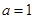 时,求函数
时,求函数 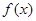 的最小值;
的最小值;
(Ⅱ)当 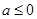 时,讨论函数
时,讨论函数 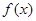 的单调性;
的单调性;
(Ⅲ)是否存在实数 ,对任意的
,对任意的  ,且
,且 ,有
,有 ,恒成立,若存在求出
,恒成立,若存在求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。