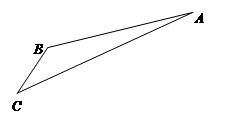
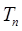如图,游客在景点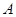 处下山至
处下山至 处有两条路径.一条是从
处有两条路径.一条是从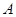 沿直道步行到
沿直道步行到 ,另一条是先从
,另一条是先从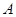 沿索道乘缆车到
沿索道乘缆车到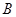 ,然后从
,然后从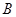 沿直道步行到
沿直道步行到 .现有甲、乙两位游客从
.现有甲、乙两位游客从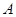 处下山,甲沿
处下山,甲沿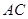 匀速步行,速度为
匀速步行,速度为 .在甲出发
.在甲出发 后,乙从
后,乙从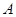 乘缆车到
乘缆车到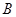 ,在
,在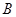 处停留
处停留 后,再从
后,再从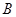 匀速步行到
匀速步行到 .假设缆车匀速直线运动的速度为
.假设缆车匀速直线运动的速度为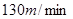 ,索道
,索道 长为
长为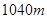 ,经测量
,经测量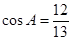 ,
, .
.
(1)求山路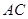 的长;
的长;
(2)假设乙先到,为使乙在 处等待甲的时间不超过
处等待甲的时间不超过 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内?
已知函数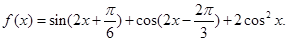
(I)求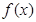 的最大值和最小正周期;
的最大值和最小正周期;
(II)若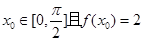 ,求
,求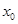 的值。
的值。
已知集合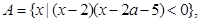 函数
函数 的定义域为集合B。
的定义域为集合B。
(I)若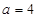 ,求集合
,求集合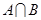 ;
;
(II)已知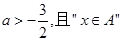 是“
是“ ”的必要条件,求实数a的取值范围。
”的必要条件,求实数a的取值范围。
、如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点。
(Ⅰ) 若PA=AB=2,求三棱锥P-ABC的体积;
(Ⅱ)证明:BE⊥平面PAC
(Ⅲ)如何在BC上找一点F,使AD//平面PEF?并说明理由。
已知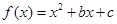 为偶函数,曲线
为偶函数,曲线 过点
过点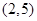 ,
, .
.
(Ⅰ)求实数b、c的值;
(Ⅱ)若曲线 有斜率为0的切线,求实数
有斜率为0的切线,求实数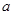 的取值范围;
的取值范围;
(Ⅲ)若当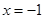 时函数
时函数 取得极值,确定
取得极值,确定 的单调区间和极值.
的单调区间和极值.
等比数列{ }的前n 项和为
}的前n 项和为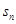 ,已知
,已知 ,
,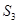 ,
,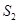 成等差数列.
成等差数列.
(Ⅰ)求{ }的公比q;
}的公比q;
(Ⅱ)求 -
- =3,求数列{
=3,求数列{ }的通项公式
}的通项公式
(Ⅲ)数列{n }的前n项的和
}的前n项的和