设命题p:函数 在(0,+
在(0,+ )上是增函数;命题q:方程
)上是增函数;命题q:方程 有两个不相等的负实数根,若p
有两个不相等的负实数根,若p q是真命题。
q是真命题。
(1)求点P(a,b)的轨迹图形的面积;
(2)求a+5b的取值范围。
(本小题满分12分) 已知函数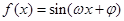 (
( ,
,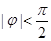 )图象的相邻两对称轴间的距离为
)图象的相邻两对称轴间的距离为 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位后图象关于
个单位后图象关于 轴对称.
轴对称.
(1)求使 成立的
成立的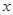 的取值范围;
的取值范围;
(2)设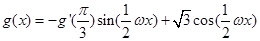 ,其中
,其中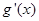 是
是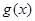 的导函数,若
的导函数,若 ,且
,且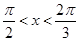 ,求
,求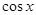 的值.
的值.
选修4—5:不等式选讲
设函数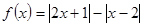
(1)求不等式 的解集;
的解集;
(2)若 恒成立,求实数
恒成立,求实数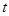 的取值范围.
的取值范围.
已知曲线C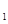 :
: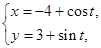 (t为参数), C
(t为参数), C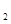 :
: (
( 为参数)。
为参数)。
(1)分别求出曲线C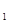 ,C
,C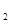 的普通方程;
的普通方程;
(2)若C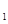 上的点P对应的参数为
上的点P对应的参数为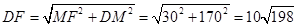 ,Q为C
,Q为C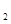 上的动点,求
上的动点,求 中点
中点 到直线
到直线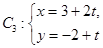 (t为参数)距离的最小值及此时Q点坐标.
(t为参数)距离的最小值及此时Q点坐标.
如图,⊙O过平行四边形ABCT的三个顶点B,C,T,且与AT相切,交AB的延长线于点D.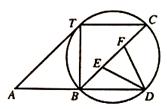
(1)求证:AT2=BT·AD;
(2)E、F是BC的三等分点,且DE=DF,求∠A.
(本小题满分12分)设函数 (
(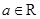 ).
).
(1)当 时,讨论函数
时,讨论函数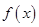 的单调性;
的单调性;
(2)若对任意 及任意
及任意 ,
,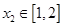 ,恒有
,恒有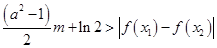 成立,求实数
成立,求实数 的取值范围.
的取值范围.