已知曲线C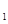 :
: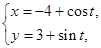 (t为参数), C
(t为参数), C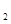 :
: (
( 为参数)。
为参数)。
(1)分别求出曲线C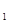 ,C
,C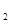 的普通方程;
的普通方程;
(2)若C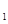 上的点P对应的参数为
上的点P对应的参数为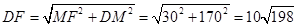 ,Q为C
,Q为C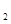 上的动点,求
上的动点,求 中点
中点 到直线
到直线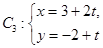 (t为参数)距离的最小值及此时Q点坐标.
(t为参数)距离的最小值及此时Q点坐标.
已知函数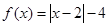 ,
,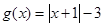 .
.
(Ⅰ)若函数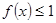 ,求
,求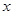 的取值范围;
的取值范围;
(Ⅱ)若不等式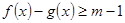 有解,求
有解,求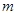 的取值范围.
的取值范围.
曲线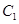 的参数方程为
的参数方程为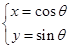 (
(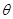 为参数),将曲线
为参数),将曲线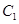 上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的
上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的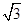 倍,得到曲线
倍,得到曲线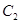 .
.
(Ⅰ)求曲线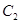 的普通方程;
的普通方程;
(Ⅱ)已知点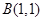 ,曲线
,曲线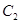 与
与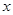 轴负半轴交于点
轴负半轴交于点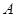 ,
,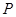 为曲线
为曲线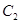 上任意一点, 求
上任意一点, 求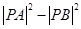 的最大值.
的最大值.
如图, ⊙O为 的外接圆,直线
的外接圆,直线 为⊙O的切线,切点为
为⊙O的切线,切点为 ,直线
,直线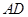 ∥
∥ ,交
,交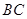 于
于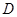 ,交⊙O于
,交⊙O于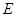 ,
, 为
为 上一点,且
上一点,且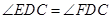 .
.
求证:(Ⅰ) ;
;
(Ⅱ)点 、
、 、
、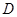 、
、 共圆.
共圆.
已知函数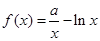 .
.
(Ⅰ)若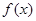 在
在 处取得极值,求实数
处取得极值,求实数 的值;
的值;
(Ⅱ)若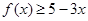 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,已知椭圆 的中心在原点,其上、下顶点分别为
的中心在原点,其上、下顶点分别为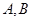 ,点
,点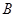 在直线
在直线 上,点
上,点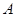 到椭圆的左焦点的距离为
到椭圆的左焦点的距离为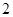 .
.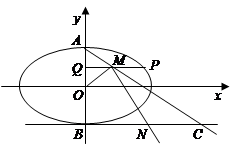
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设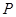 是椭圆上异于
是椭圆上异于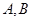 的任意一点,点
的任意一点,点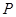 在
在 轴上的射影为
轴上的射影为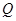 ,
,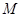 为
为 的中点,直线
的中点,直线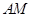 交直线
交直线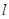 于点
于点 ,
,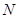 为
为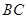 的中点,试探究:
的中点,试探究: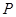 在椭圆上运动时,直线
在椭圆上运动时,直线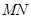 与圆
与圆 :
: 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.