设抛物线 的焦点为
的焦点为 ,准线为
,准线为 ,
, ,以
,以 为圆心的圆
为圆心的圆 与
与 相切于点
相切于点 ,
, 的纵坐标为
的纵坐标为 ,
, 是圆
是圆 与
与 轴除
轴除 外的另一个交点.
外的另一个交点.
(I)求抛物线 与圆
与圆 的方程;
的方程;
( II)已知直线 ,
, 与
与 交于
交于 两点,
两点, 与
与 交于点
交于点 ,且
,且 , 求
, 求 的面积.
的面积.
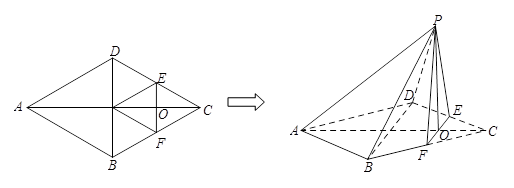
如图,在边长为4的菱形 中,
中,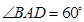 ,点
,点 、
、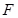 分别在边
分别在边 、
、 上.点
上.点 与点
与点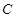 、
、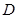 不重合,
不重合, ,
,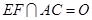 ,沿
,沿 将
将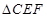 翻折到
翻折到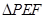 的位置,使平面
的位置,使平面 平面
平面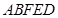 .
.
(1)求证: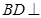 平面
平面 ;
;
(2)记三棱锥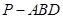 的体积为
的体积为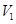 ,四棱锥
,四棱锥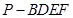 的体积为
的体积为 ,且
,且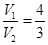 ,求此时线段
,求此时线段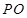 的长.
的长.
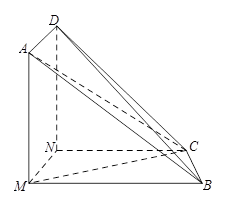
如图所示,在三棱锥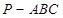 中,
中,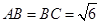 ,平面
,平面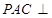 平面
平面 ,
,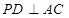 于点
于点 ,
, 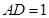 ,
,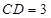 ,
, .
.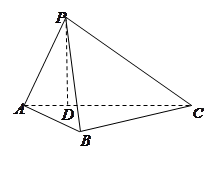
(1)求三棱锥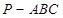 的体积;
的体积;
(2)证明 为直角三角形.
为直角三角形.
如图,在直三棱柱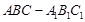 中,
中,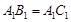 ,
,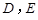 分别是棱
分别是棱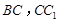 上的点(点
上的点(点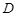 不同于点
不同于点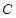 ),且
),且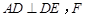 为
为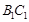 的中点.
的中点.
求证:(1)平面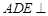 平面
平面 ;
;
(2)直线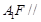 平面
平面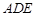 .
.
如图所示,在四棱锥 中,
中, 平面
平面 ,
, ∥
∥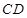 ,
,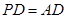 ,
, 是
是 中点,
中点,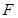 是
是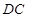 上的点,且
上的点,且 ,
,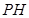 为
为 中
中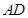 边上的高.
边上的高.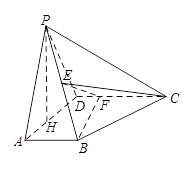
(1)证明: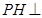 平面
平面 ;
;
(2)若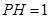 ,
,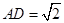 ,
,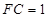 ,求三棱锥
,求三棱锥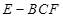 的体积;
的体积;
(3)证明: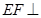 平面
平面 .
.
如图,矩形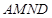 所在的平面与直角梯形
所在的平面与直角梯形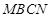 所在的平面互相垂直,
所在的平面互相垂直,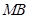 ∥
∥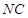 ,
,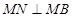 .
.
(1)求证:平面 ∥平面
∥平面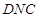 ;
;
(2)若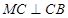 ,求证
,求证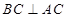 .
.