在“极限”运动会中，有一个在钢索桥上的比赛项目。如图所示，总长为L的均匀粗钢丝绳固定在等高的A、B处，钢丝绳最低点与固定点A、B的高度差为H，动滑轮起点在A处，并可沿钢丝绳滑动，钢丝绳最低点距离水面也为H。若质量为m的人抓住滑轮下方的挂钩由A点静止滑下，最远能到达右侧C点，C、B间钢丝绳相距为
，高度差为
。若参赛者在运动过程中始终处于竖直状态，抓住滑轮的手与脚底之间的距离也为
，滑轮与钢丝绳间的摩擦力大小视为不变，且摩擦力所做功与滑过的路程成正比，不计参赛者在运动中受到的阻力、滑轮（含挂钩）的质量和大小，不考虑钢索桥的摆动及形变。
（1）滑轮与钢丝绳间的摩擦力是多大？
（2）若参赛者不依靠外界帮助要到达B点，则人在A点处抓住挂钩时至少应该具有多大的初动能？
（3）比赛规定参赛者须在钢丝绳最低点脱钩并到达与钢丝绳最低点水平相距为
、宽度为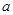
，厚度不计的海绵垫子上。若参赛者由A点静止滑下，会落在海绵垫子左侧的水中。为了能落到海绵垫子上，参赛者在A点抓住挂钩时应具有初动能的范围？
图中虚线MN是一垂直纸面的平面与纸面的交线，在平面右侧的半空间存在一磁感强度为B的匀强磁场，方向垂直纸面向外。O是MN上的一点，从O点可以向磁场区域发射电量为+q、质量为m、速率为v的粒子，粒子射入磁场时的速度可在纸面内各个方向。已知先后射入的两个粒子恰好在磁场中给定的P点相遇，P到O的距离为L。不计重力及粒子间的相互作用。
(1)求所考察的粒子在磁场中的轨道半径。
(2)求这两个粒子从O点射入磁场的时间间隔。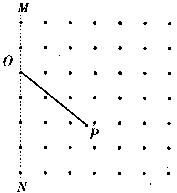
质量为0.1 kg的弹性小球从高1.25 m处自由下落至一光滑而坚硬的水平板上，碰撞后弹回到0.8 m高处，求：
（1）小球与水平板碰撞前后的动量；（2）小球与水平板碰撞前后的动量变化。（g="10" m/s2）
如图所示，总质量为m的飞船绕地球在半径为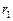
的圆轨道I上运行，要进入半径为
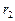的更高的圆轨道II，必须先加速进入一个椭圆轨道III，然后再进入圆轨道II。轨道I、III相切于A点。已知飞船在圆轨道II上运动速度大小为
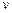，在A点通过发动机向后以速度大小为
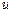（对地）喷出一定质量气体，使飞船速度增加到
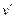进入椭圆轨道III。（已知量为
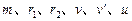）求：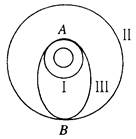
（1）飞船在轨道I上的速度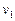
；（2）发动机喷出气体的质量。
如图，一绝缘细圆环半径为r，环面处于水平面内，场强为E的匀强电场与圆环平面平行。环上穿有一电量为＋q、质量为m的小球，可沿圆环做无摩擦的圆周运动。若小球经A点时速度的方向恰与电场垂直，且圆环与小球间沿水平方向无力的作用（设地球表面重力加速度为g）。则：
（1）小球经过A点时的速度大小vA是多大？
（2）当小球运动到与A点对称的B点时，小球的速度是多大？圆环对小球的作用力大小是多少？
如图所示，在竖直放置的铅屏A的右表面上贴着
射线放射源P，已知射线实质为高速电子流，放射源放出粒子的速度v0＝1.0
m/s。足够大的荧光屏M与铅屏A平行放置，相距d＝0.02m，其间有水平向左的匀强电场，电场强度大小E＝2.5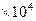
N/C。已知电子电量e＝1.6
C，电子质量取m＝9.0
kg。求
（1）电子到达荧光屏M上的动能；
（2）荧光屏上的发光面积。