已知平面内一动点P到点F(1，0)的距离与点P到y轴的距离的差等于1．
（Ⅰ）求动点P的轨迹C的方程；
（Ⅱ）过点F作两条斜率存在且互相垂直的直线l1，l2，设l1与轨迹C相交于点A，B，l2与轨迹C相交于点D，E，求
的最小值．
如下图，某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b. 
(1)求这段时间的最大温差.
(2)写出这段曲线的函数解析式.
不查表求sin220°+cos280°+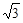
sin20°cos80°的值.
已知α、β为锐角，且x(α+β－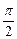
)＞0,试证不等式f(x)=
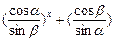x＜2对一切非零实数都成立.
如右图，一滑雪运动员自h=50m高处A点滑至O点，由于运动员的技巧(不计阻力)，在O点保持速率v0不为，并以倾角θ起跳，落至B点，令OB=L，试问，α=30°时，L的最大值为多少？当L取最大值时，θ为多大？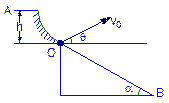
从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业，根据规划，本年度投入800万元，以后每年投入将比上年减少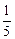
，本年度当地旅游业收入估计为400万元，由于该项建设对旅游业的促进作用，预计今后的旅游业收入每年会比上年增加
.
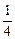(1)设n年内(本年度为第一年)总投入为an万元，旅游业总收入为bn万元，写出an,bn的表达式；
(2)至少经过几年，旅游业的总收入才能超过总投入？